题目内容
5.设函数f(x)=ax2-bx+3,y=f(x)在x∈(-∞,1]单调递增,在x∈[1,+∞)单调递减,且有最大值4.(1)求函数f(x)的表达式;
(2)设$g(x)=\frac{f(x)}{x}$若g(2+sinθ)≥m2-m对任意θ∈R恒成立,则实数m的取值范围.
分析 (1)根据一元二次函数的性质建立不等式关系进行求解即可.
(2)判断函数g(x)的单调性,利用参数分离法进行求解即可.
解答 解:∵y=f(x)在x∈(-∞,1]单调递增,在x∈[1,+∞)单调递减,且有最大值4,
∴$\left\{{\begin{array}{l}{-\frac{-b}{2a}=1}\\{a-b+3=4}\end{array}}\right.$解得:$\left\{{\begin{array}{l}{a=-1}\\{b=-2}\end{array}}\right.$…..(3分),
∴f(x)=-x2+2x+3…..(4分)
(2)由(1)$g(x)=\frac{{-{x^2}+2x+3}}{x}$=$\frac{3}{x}-x+2$,
则g′(x)=-$\frac{3}{{x}^{2}}$-1<0恒成立,
∵θ∈R,
∴-1≤sinθ≤1,1≤2+sinθ≤3…..(5分)
∴g(x)在[1,3]上是单调减函数…..(9分),
∴当g(2+sinθ)min=g(3)=0…..(10分)
∴m2-m≤0,
∴0≤m≤1…(12分)
点评 本题主要考查函数解析式的求解,以及不等式恒成立问题,利用参数分离法结合函数的最值问题是解决本题的关键.

练习册系列答案
相关题目
13.已知向量$\overrightarrow a=(0,-1),\overrightarrow b=(2,m)$,若$\overrightarrow a,\overrightarrow b$的夹角为$\frac{π}{4}$,则m的值为( )
| A. | -1 | B. | -2 | C. | ±1 | D. | ±2 |
20.在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线y=f(x)(实线表示),另一种是平均价价格曲线y=g(x)(虚线表示)(如f(2)=3是指开始买卖后两个小时的即时价格为3元g(2)=3表示2个小时内的平均价格为3元),如图给出四个图象:
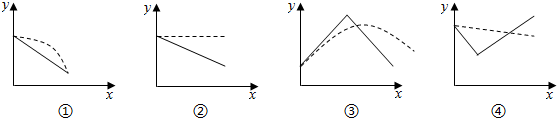
其中可能正确的图象序号是( )

其中可能正确的图象序号是( )
| A. | ①②③④ | B. | ③ | C. | ①③ | D. | ①③④ |
14.若sin2α>0,则( )
| A. | cosα>0 | B. | tanα>0 | C. | sinα>0 | D. | cos2α>0 |
 如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且FD=$\sqrt{3}$.
如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且FD=$\sqrt{3}$. 如图,已知直线与抛物线y2=2px(p>0)交于M,N两点,点D的坐标为$({1,\sqrt{3}})$,OD⊥MN交MN于点D,OM⊥ON,抛物线的焦点为F.
如图,已知直线与抛物线y2=2px(p>0)交于M,N两点,点D的坐标为$({1,\sqrt{3}})$,OD⊥MN交MN于点D,OM⊥ON,抛物线的焦点为F.