题目内容
4.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{x},x≥0}\\{-{x}^{2}-3x,x<0}\end{array}\right.$,若f(x)≤2,则x的取值范围是(-∞,-2]∪[-1,4].分析 在每段上解不等式f(x)≤2,然后所得x的范围求并集即可得出x的取值范围.
解答 解:(1)当x≥0时,由f(x)≤2得,$\sqrt{x}≤2$;
∴0≤x≤4;
(2)当x<0时,由f(x)≤2得,-x2-3x≤2;
解得x≤-2,或-1≤x<0;
综上得,x的取值范围是(-∞,-2]∪[-1,4].
故答案为:(-∞,-2]∪[-1,4].
点评 考查分段函数的概念,对于分段函数,解不等式f(x)≤2时,在每段上去解,无理不等式和一元二次不等式的解法.

练习册系列答案
相关题目
19.已知点P(x,y)在不等式组$\left\{\begin{array}{l}{x-2≤0}\\{y-1≤0}\\{x+2y-2≥0}\end{array}\right.$表示的平面区域上运动,则z=x2+y2的取值范围是( )
| A. | [$\frac{3}{5}$,4] | B. | [$\frac{4}{5}$,5] | C. | [$\frac{4}{5}$,6] | D. | [$\frac{3}{5}$,5] |
13.函数y=$\left\{\begin{array}{l}{2x}&{x≥0}\\{-{x}^{2}}&{x<0}\end{array}\right.$的反函数是( )
| A. | y=$\left\{\begin{array}{l}{\frac{x}{2}}&{x≥0}\\{\sqrt{-x}}&{x<0}\end{array}\right.$ | B. | y=$\left\{\begin{array}{l}{\frac{x}{2}}&{x≥0}\\{-\sqrt{-x}}&{x<0}\end{array}\right.$ | ||
| C. | y=$\left\{\begin{array}{l}{2x}&{x≥0}\\{\sqrt{-x}}&{x<0}\end{array}\right.$ | D. | y=$\left\{\begin{array}{l}{2x}&{x≥0}\\{-\sqrt{-x}}&{x<0}\end{array}\right.$ |
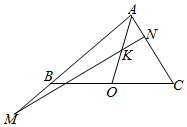 如图所示,在△ABC中,AO是BC边上的中线,K为AO上一点,且$\overrightarrow{AO}$=2$\overrightarrow{AK}$,过点K的直线分别交直线AB、AC于不同的两点M,N,若$\overrightarrow{AB}$=m$\overrightarrow{AM}$,$\overrightarrow{AC}$=n$\overrightarrow{AN}$,则m+n=4.
如图所示,在△ABC中,AO是BC边上的中线,K为AO上一点,且$\overrightarrow{AO}$=2$\overrightarrow{AK}$,过点K的直线分别交直线AB、AC于不同的两点M,N,若$\overrightarrow{AB}$=m$\overrightarrow{AM}$,$\overrightarrow{AC}$=n$\overrightarrow{AN}$,则m+n=4.