题目内容
已知椭圆C1: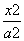 +
+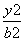 =1(a>b>0)与圆C2:x2+y2=b2,若在椭圆C1上存在点P,使得由点P所作的圆C2的两条切线互相垂直,则椭圆C1的离心率的取值范围是( )
=1(a>b>0)与圆C2:x2+y2=b2,若在椭圆C1上存在点P,使得由点P所作的圆C2的两条切线互相垂直,则椭圆C1的离心率的取值范围是( )
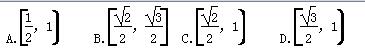
C
[解析] 由椭圆上长轴端点向圆作两条切线PA,PB,则两切线形成的角∠APB最小,若椭圆C1上存在点P令切线互相垂直,则只需∠APB≤90°,即α=∠APO≤45°,∴sin α= ≤sin 45°=
≤sin 45°=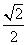 ,解得a2≤2c2,∴e2≥
,解得a2≤2c2,∴e2≥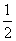 ,即e≥
,即e≥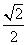 ,而0<e<1,∴
,而0<e<1,∴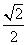 ≤e<1,即e∈
≤e<1,即e∈ .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的图象关于直线
的图象关于直线 对称,则
对称,则 = ______________
= ______________ ,
, ,则
,则
 .
. ,则p=( )
,则p=( )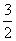
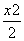 +y2=1的左焦点,点P为椭圆C上任意一点,点Q的坐标为(4,3),则|PQ|+|PF|取最大值时,点P的坐标为________.
+y2=1的左焦点,点P为椭圆C上任意一点,点Q的坐标为(4,3),则|PQ|+|PF|取最大值时,点P的坐标为________. 是定义在R上的可导函数,且当
是定义在R上的可导函数,且当 时,
时, ,则关于
,则关于 的函数
的函数 的零点个数为( )
的零点个数为( )