题目内容
1.已知直线l过抛物线x=$\frac{1}{4}$y2的焦点F且与抛物线交于点A,B.(1)求证:$\overrightarrow{OA}$•$\overrightarrow{OB}$<0;
(2)当l斜率为$\frac{1}{2}$时,抛物线上是否存在点C使得△ABC是以C为直角的直角三角形?若存在,求出所有的点C,若不存在,说明理由.
分析 (1)设直线AB的方程为x=my+1,代入抛物线方程得y2-4my-4=0,利用韦达定理可证明;
(2)由已知可求得AB方程,与抛物线方程联立求得A,B坐标,假设抛物线上存在点C(t2,2t)使△ABC为直角三角形且C为直角,由$\overrightarrow{CA}$•$\overrightarrow{CB}$=0可求得t值,从而可求得C点坐标,经验证可得答案.
解答 (1)证明:由题意知,抛物线x=$\frac{1}{4}$y2的焦点坐标为( 1,0),
设直线AB的方程为x=my+1,
代入抛物线方程得y2-4my-4=0,
设A(x1,y1),B(x2,y2),则y1+y2=4m,y1•y2=-4,
x1•x2=m2y1•y2+m(y1+y2)+1=1
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1•x2+y1•y2=-3<0;
(2)解:AB方程:x-2y-1=0,代入抛物线y2=4x,求得A(9+4$\sqrt{5}$,4+2$\sqrt{5}$),B(9-4$\sqrt{5}$,4-2$\sqrt{5}$),
假设抛物线上存在点C(t2,2t)使△ABC为直角三角形且C为直角,
此时$\overrightarrow{CA}$•$\overrightarrow{CB}$=0,所以t4-34t2-3=0,解得t2=17+2$\sqrt{73}$
则存在C(17+2$\sqrt{73}$,$\sqrt{17+2\sqrt{73}}$)使△ABC为直角三角形且C为直角.
点评 本题考查直线与圆锥曲线的位置关系及椭圆方程的求解,考查向量在判断三角形形状中的应用,考查学生灵活运用所学知识分析解决问题的能力,属于中档题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
11.已知直线x+y-a=0(a>0)与圆x2+y2=4交于不同的两点A,B,O是坐标原点,且有|$\overrightarrow{OA}$+$\overrightarrow{OB}$|≥|$\overrightarrow{AB}$|,那么a的取值范围是( )
| A. | ($\sqrt{2}$,+∞) | B. | 2,+∞) | C. | [2,2$\sqrt{2}$) | D. | [$\sqrt{2}$,2$\sqrt{2}$) |
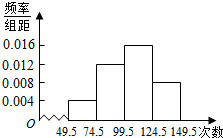 为了调查学生的课外阅读情况,在某班级对全体学生每天阅读时间(单位:分钟)进行调查,将调查数据整理后,画出频率分布直方图如图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第三组的频数为20.
为了调查学生的课外阅读情况,在某班级对全体学生每天阅读时间(单位:分钟)进行调查,将调查数据整理后,画出频率分布直方图如图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第三组的频数为20.