题目内容

12．已知y=f（x）的导函数为y=f'（x），且在x=1处的切线方程为y=-x+3，则f（1）-f'（1）=（　　）
A．2B．3C．4D．5

分析 由已知切线的方程，结合导数的几何意义：函数在某点处的导数即为曲线在该点处切线的斜率，计算即可得到所求值．

解答 解：由f（x）在x=1处的切线方程为y=-x+3，
可得则f（1）-f'（1）=3-1-（-1）=3．
故选：B．

点评 本题考查导数的几何意义：函数在某点处的导数即为曲线在该点处切线的斜率，考查运算能力，属于基础题．

练习册系列答案
相关题目
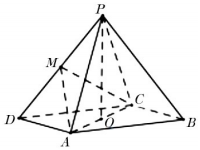2．如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠ADC=45°，AD=AC=2，O为AC的中点，PO⊥平面ABCD且PO=6，M为BD的中点．
（1）证明：AD⊥平面PAC；
（2）求直线AM与平面ABCD所成角的正切值．
3．已知$|\overrightarrow a|=3，|\overrightarrow{b|}=4$，且$|\overrightarrow a|$与$|\overrightarrow{b|}$为不共线的平面向量．
（1）若$（\overrightarrow a+k\overrightarrow b）⊥（\overrightarrow a-k\overrightarrow b）$，求k的值；
（2）若$（k\overrightarrow a-4\overrightarrow b）$∥$（\overrightarrow a-k\overrightarrow b）$，求k的值．
20．计算：$lg4+lg9+2\sqrt{{{（{lg6}）}^2}-lg36+1}$=2．
7．已知以点A（-1，2）为圆心的圆与直线l1：x+2y+7=0相切，过点B（-4，0）的动直线l与圆A相交于M，N两点．
（1）求圆A的方程；
（2）当$|{MN}|=2\sqrt{11}$时，求直线l的方程．
17．已知函数f（x）=sin（ωx+φ）-b（ω＞0，0＜φ＜π）的图象两相邻对称轴之间的距离是$\frac{π}{2}$，若将f（x）的图象先向右平移$\frac{π}{6}$个单位，再向上平移$\sqrt{3}$个单位，所得函数g（x）为奇函数．
（1）求f（x）的解析式；
（2）求f（x）的对称轴及单调区间．
4．设f0（x）=sinx，f1（x）=f0′（x），f2（x）=f1′（x），…，fn+1（x）=fn′（x），n∈N，则f2017（x）=（　　）
A．sinxB．-sinxC．cosxD．-cosx
1．设函数f（x）=axlnx+$\frac{1}{x}$（a＞0）．
（Ⅰ）当a=1时，讨论f（x）的单调性；
（Ⅱ）设g（x）=f（x）-ax，若g（x）≥0恒成立，求a的取值范围．
20．已知Sn为等比数列{an}的前n项和，且Sn=3n+r．
（1）求r的值，并求数列的通项公式an；
（2）若bn=$\frac{{a}_{n}}{{S}_{n}{S}_{n+1}}$，求数列{bn}前n项和Tn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网