题目内容
下列各组函数是同一函数的是
- A.y=
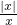 与y=1
与y=1 - B.y=|x-1|与
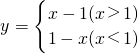
- C.y=|x|+|x-1|与y=2x-1
- D.y=
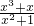 与y=x
与y=x
D
分析:本题考查的知识点是判断两个函数是否为同一函数,逐一分析四个答案中两个函数的定义域与解析式,判断是否一致,然后根据函数相同的定义判断即可得到答案.
解答:∵A中,y= ,定义域与对应法则都不同,∴排除A.
,定义域与对应法则都不同,∴排除A.
又∵B中,y=|x-1|= ,定义域不同,∴排除B.
,定义域不同,∴排除B.
∵C中,y=|x|+|x-1|= 对应法则不同,∴排除C.
对应法则不同,∴排除C.
D中、y=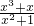 =
= =x,与y=x定义域和对应法则均相同,为同一函数;
=x,与y=x定义域和对应法则均相同,为同一函数;
故选D.
点评:判断两个函数是否为同一函数,我们要分别判断两个函数的定义域和对应法则(解析式)是否相同,只有两者都相同的函数才是同一函数.
分析:本题考查的知识点是判断两个函数是否为同一函数,逐一分析四个答案中两个函数的定义域与解析式,判断是否一致,然后根据函数相同的定义判断即可得到答案.
解答:∵A中,y=
 ,定义域与对应法则都不同,∴排除A.
,定义域与对应法则都不同,∴排除A.又∵B中,y=|x-1|=
 ,定义域不同,∴排除B.
,定义域不同,∴排除B.∵C中,y=|x|+|x-1|=
 对应法则不同,∴排除C.
对应法则不同,∴排除C.D中、y=
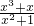 =
= =x,与y=x定义域和对应法则均相同,为同一函数;
=x,与y=x定义域和对应法则均相同,为同一函数;故选D.
点评:判断两个函数是否为同一函数,我们要分别判断两个函数的定义域和对应法则(解析式)是否相同,只有两者都相同的函数才是同一函数.

练习册系列答案
相关题目
下列各组函数是同一函数的是( )
①f(x)=
与g(x)=x
;
②f(x)=|x|与g(x)=
;
③f(x)=x0与g(x)=1;
④f(x)=x2-2x-1与g(t)=t2-2t-1.
①f(x)=
| -2x3 |
| -2x |
②f(x)=|x|与g(x)=
| x2 |
③f(x)=x0与g(x)=1;
④f(x)=x2-2x-1与g(t)=t2-2t-1.
| A、①② | B、①③ | C、②④ | D、③④ |
下列各组函数是同一函数的是( )
①f(x)=
与g(x)=x
;
②f(x)=x与g(x)=
;
③f(x)=x0与g(x)=
;
④f(x)=x2-2x-1与g(t)=t2-2t-1.
①f(x)=
| -2x3 |
| -2x |
②f(x)=x与g(x)=
| x2 |
③f(x)=x0与g(x)=
| 1 |
| x0 |
④f(x)=x2-2x-1与g(t)=t2-2t-1.