题目内容
已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,动点M到圆C的切线长与|MQ|的比等于常数λ(λ>0),求动点M的轨迹方程,并说明它表示什么曲线.
解析:设切点为N,则|MN|=λ|MQ|.
于是|MO|2-r2=(λ|MQ|)2.
将M(x,y)代入上式,得x2+y2-1=λ2(x-2)2+λ2y2,
整理得(λ2-1)(x2+y2)-4λ2x+(1+4λ2)=0.
当λ=1时,方程为x=
,表示一直线.?
当λ≠1时,方程为
,表示一个圆.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
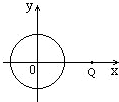已知直角坐标平面上点Q（2，0）和圆C：x2+y2=1，动点M到圆C的切线长与|MQ|的比等于常数λ（λ＞0）．求动点M的轨迹方程，说明它表示什么曲线．
已知直角坐标平面上点Q（k，0）和圆C：x2+y2=1；动点M到圆的切线长与Q|
如图，已知直角坐标平面上点Q（2，0）和圆C：x2+y2=1，动点M到圆C的切线长与|MQ|的比等于