Question

已知直角坐标平面上点Q（k，0）和圆C：x²+y²=1；动点M到圆的切线长与Q|
的比值为2．
（1）当 k=2 时，求点M 的轨迹方程．
（2）当 k∈R 时，求点M 的轨迹方程，并说明轨迹是什么图形．

Answer 1

分析：（1）设出M的坐标，通过解直角三角形表示出切线长，利用两点距离公式表示出|MQ|的长，利用已知条件及k=2求出点M 的轨迹方程．
（2）先求出轨迹方程，通过配方化简方程，通过对等式右边的式子分类讨论得到动点的轨迹．

解答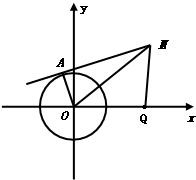：设点M的坐标为（x，y）
则点M到圆的切线长|MA|=

MO2-AO2

=

x2+y2-1

|MQ|=

(x-k)2+y2

（1）当k=2时，

|MA|

|MQ|

=

x2+y2-1

(x-2)2+y2

=2
化简得3x²+3y²-16x+17=0即为点M的轨迹方程．
（2）当k∈R时

|MA|

|MQ|

=

x2+y2-1

(x-k)2+y2

=2，
∴x²+y²-1=4[（x-k）²+y²]
化简得点M的轨迹方程为：3x²+3y²-8kx+4k²+1=0
整理得：x2+y2-

8

3

kx+

4k2+1

3

=0即(x-

4

3

k)2+y2=

4k2-3

9

∴k＞

3

2

或k＜-

3

2

时，点M的轨迹是以(

4k

3

，0)为圆心，以

4k2-3

3

为半径的圆；
k=

3

2

或k=-

3

2

时，点M的轨迹是点(

4k

3

，0)；-

3

2

＜k＜

3

2

时，该方程不代表任何图形．

点评：本题考查求圆的切线长的方法、直接法求动点的轨迹方程、分类讨论的数学方法．