Question

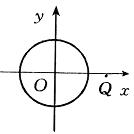
如图，已知直角坐标平面上点Q（2，0）和圆C：x²+y²=1，动点M到圆C的切线长与|MQ|的比等于

2

．求动点M的轨迹方程，并说明它表示什么曲线．

Answer 1

分析：根据动点M到圆C的切线长与|MQ|的比等于

2

，可建立方程，两边平方，化简即可

解答：解：如图，设直线 MN切圆于N，则动点M组成的集合是：P={M||MN|=

2

|MQ|}．
因为圆的半径|ON|=1，所以|MN|²=|MO|²-1
设点 M的坐标为 （x，y），
则

x2+y2-1

=

2

(x-2)2+y2

整理得（x-4）²+y²=7
它表示圆，该圆圆心的坐标为（4，0），半径为

7

                                                                                               

点评：本题考查轨迹方程的求法，考查方程与曲线的关系，解题时要注意公式的灵活运用，仔细分析，认真求解．