题目内容
已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,动点M到圆C的切线长与|MQ|的比等于常数2,求动点M的轨迹方程,说明它表示什么曲线.
分析:由题意列出动点M所满足的集合,把|MN|用|OM|和常数表示,设出M的坐标后代入M所满足的关系式,整理后即可得到答案.
解答: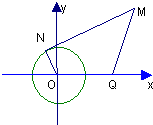 解:如图,设MN切圆于N,则动点M组成的集合是P={M||MN|=2|MQ|}
解:如图,设MN切圆于N,则动点M组成的集合是P={M||MN|=2|MQ|}
∵圆的半径|ON|=1
∴|MN|2=|MO|2-|ON|2=|MO|2-1
设点M的坐标为(x,y),
则
=2
整理得3(x2+y2)-16x+17=0,即x2+y2-
x+
=0
它表示圆心为(
,0),半径为
的圆.
 解:如图,设MN切圆于N,则动点M组成的集合是P={M||MN|=2|MQ|}
解:如图,设MN切圆于N,则动点M组成的集合是P={M||MN|=2|MQ|}∵圆的半径|ON|=1
∴|MN|2=|MO|2-|ON|2=|MO|2-1
设点M的坐标为(x,y),
则
| x2+y2-1 |
| (x-2)2+y2 |
整理得3(x2+y2)-16x+17=0,即x2+y2-
| 16 |
| 3 |
| 17 |
| 3 |
它表示圆心为(
| 8 |
| 3 |
| 13 |
| 3 |
点评:本题考查了轨迹方程的求法,考查了直线与圆的关系,求解轨迹方程问题的关键步骤是列出动点所满足的关系式,是中档题.

练习册系列答案
相关题目
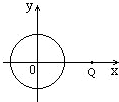 已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,动点M到圆C的切线长与|MQ|的比等于常数λ(λ>0).求动点M的轨迹方程,说明它表示什么曲线.
已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,动点M到圆C的切线长与|MQ|的比等于常数λ(λ>0).求动点M的轨迹方程,说明它表示什么曲线. 已知直角坐标平面上点Q(k,0)和圆C:x2+y2=1;动点M到圆的切线长与Q|
已知直角坐标平面上点Q(k,0)和圆C:x2+y2=1;动点M到圆的切线长与Q| 如图,已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,动点M到圆C的切线长与|MQ|的比等于
如图,已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,动点M到圆C的切线长与|MQ|的比等于