题目内容
3.已知$f(x)=\left\{\begin{array}{l}{x^2}-4x+3,\;\;x≤0\\-{x^2}-2x+3,\;\;x>0\end{array}\right.$,当x∈[a,a+1]时不等式f(x+a)≥f(2a-x)恒成立,则实数a的最大值是-2.分析 根据分段函数,讨论其单调性,根据单调性得出a≥2x在x∈[a,a+1]时恒成立,只需求出右式的最大值即可.
解答 解:二次函数x2-4x+3的对称轴是x=2;
∴该函数在(-∞,0]上单调递减;
∴x2-4x+3≥3;
同样可知函数-x2-2x+3在(0,+∞)上单调递减;
∴-x2-2x+3<3;
∴f(x)在R上单调递减;
∴x+a≤2a-x恒成立,
∴a≥2x在x∈[a,a+1]时恒成立,
∴a≤-2,
故答案为-2.
点评 考查了分段函数的单调性判断和恒成立问题的转换.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
13.抛物线x2=4y上与焦点的距离等于4的点的纵坐标是( )
| A. | l | B. | K | C. | 3 | D. | y-1=k(x-2) |
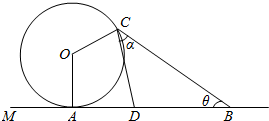 如图,在一条景观道的一端有一个半径为50米的圆形摩天轮O,逆时针15分钟转一圈,从A处进入摩天轮的座舱,OA垂直于地面AM,在距离A处150米处设置了一个望远镜B.
如图,在一条景观道的一端有一个半径为50米的圆形摩天轮O,逆时针15分钟转一圈,从A处进入摩天轮的座舱,OA垂直于地面AM,在距离A处150米处设置了一个望远镜B. 已知抛物线C:y2=2px(p>0)和两条平行线l1,l2,l1过原点O分别交曲线C和C的准线于点P,Q,l2过曲线C的焦点F,交C于点A,B.
已知抛物线C:y2=2px(p>0)和两条平行线l1,l2,l1过原点O分别交曲线C和C的准线于点P,Q,l2过曲线C的焦点F,交C于点A,B.