题目内容
点A是x轴上的动点,一条直线经过点M(2,3),垂直于MA,且交y轴于点B,过点A、B分别作x轴、y轴的垂线交于点P,求点P的轨迹方程.
考点:轨迹方程
专题:综合题,直线与圆
分析:利用MA⊥MB,可得kMA•k MB=-1,建立方程,即可求点P的轨迹方程.
解答:
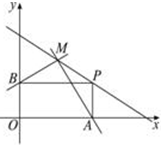 解:如图,因为PA⊥x轴,点P的坐标为(x,y),所以设点A的坐标为(x,0).因为PB⊥x轴,所以点B的坐标是(0,y).
解:如图,因为PA⊥x轴,点P的坐标为(x,y),所以设点A的坐标为(x,0).因为PB⊥x轴,所以点B的坐标是(0,y).
由已知,kMA=
(x≠2),kMB=
.
因为MA⊥MB,所以kMA•k MB=-1,
即
•
=-1 (x≠2).
化简得2x+3y-13=0.
当y=2时,由2x+3y-13=0,知y=3,点P与点M重合.
综合以上,知点P的坐标(x,y)所满足的条件是2x+3y-13=0.
 解:如图,因为PA⊥x轴,点P的坐标为(x,y),所以设点A的坐标为(x,0).因为PB⊥x轴,所以点B的坐标是(0,y).
解:如图,因为PA⊥x轴,点P的坐标为(x,y),所以设点A的坐标为(x,0).因为PB⊥x轴,所以点B的坐标是(0,y).由已知,kMA=
| 3 |
| 2-x |
| 3-y |
| 2 |
因为MA⊥MB,所以kMA•k MB=-1,
即
| 3 |
| 2-x |
| 3-y |
| 2 |
化简得2x+3y-13=0.
当y=2时,由2x+3y-13=0,知y=3,点P与点M重合.
综合以上,知点P的坐标(x,y)所满足的条件是2x+3y-13=0.
点评:本题考查求点P的轨迹方程,考查斜率的计算,考查学生的计算能力,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
下列四个函数中,在(0,+∞)上为增函数的是( )
A、y=(
| ||
| B、y=x2-3x | ||
C、y=-
| ||
| D、y=-|x| |
若x,y满足约束条件
,则3x+5y的取值范围是( )
|
| A、[-5,3] |
| B、[3,5] |
| C、[-3,3] |
| D、[-3,5] |