题目内容
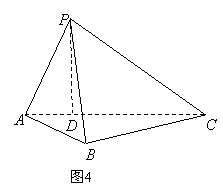
如图,在四棱锥 中,
中,
 平面
平面 ,底面
,底面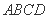 是菱形,
是菱形,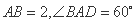 .
.
(Ⅰ) 求证: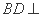 平面
平面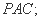
(Ⅱ)若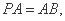 求
求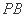 与
与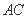 所成角的余弦值;
所成角的余弦值;
(Ⅲ)当平面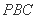 与平面
与平面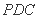 垂直时,求
垂直时,求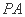 的长.
的长.

解:证明:(Ⅰ)因为四边形ABCD是菱形,
又因为PA⊥平面ABCD.
所以PA⊥BD. 又因为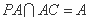
所以BD⊥平面PAC.
(Ⅱ)设AC∩BD=O.
因为∠BAD=60°,PA=AB=2,
所以BO=1,AO=CO=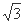 .
.
以O为坐标原点,OB为X轴,OC为Y轴建立空间直角坐标系O—xyz,则
P(0,—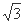 ,2),A(0,—
,2),A(0,—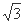 ,0),B(1,0,0),C(0,
,0),B(1,0,0),C(0,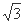 ,0).
,0).
所以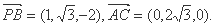
设PB与AC所成角为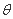 ,则
,则
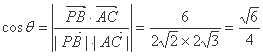 .
.
(Ⅲ)由(Ⅱ)知
设P(0,-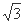 ,t)(t>0),则
,t)(t>0),则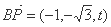 设平面PBC的法向量
设平面PBC的法向量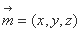 ,
,
则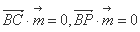
所以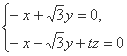 取
取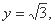 则
则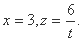 所以
所以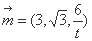
同理,平面PDC的法向量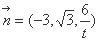
因为平面PCB⊥平面PDC,所以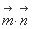 =0,即
=0,即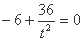
解得 ,所以PA=
,所以PA=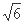

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 :“若
:“若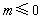 ,则
,则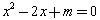 有实数解”的逆命题;命题
有实数解”的逆命题;命题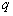 :“若函数
:“若函数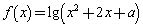 的值域为
的值域为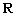 ,则
,则 ”.以下四个结论:
”.以下四个结论: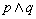 是假命题;③
是假命题;③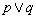 是假命题;④
是假命题;④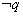 为假命题.
为假命题.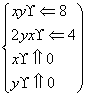 且z=5y-x的最大值为a,最小值为b,
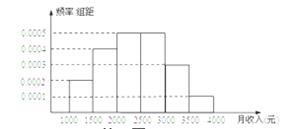
且z=5y-x的最大值为a,最小值为b,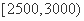 (元)月收入段应抽出
(元)月收入段应抽出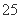 B.
B.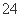 C.
C.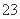 D.
D.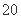
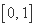 内随机的取两个数
内随机的取两个数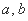 ,则满足
,则满足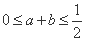 的概率是 ;(用数字作答)
的概率是 ;(用数字作答) ,
,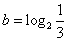 ,
, ,则( )
,则( )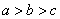 B.
B.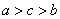 C.
C. D.
D.
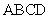 的边长为
的边长为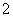 ,
,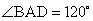 ,点
,点 ,
,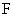 分别在边
分别在边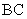 ,
,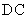 上,
上,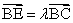 ,
,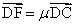 .若
.若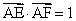 ,
,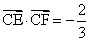 ,则
,则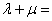 ( )
( )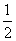 B.
B.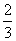 C.
C.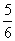 D.
D.
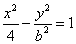 的右焦点与抛物线
的右焦点与抛物线 的焦点重合,则该双曲线的焦点到其渐近线的距离等于( )
的焦点重合,则该双曲线的焦点到其渐近线的距离等于( )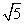 B.
B.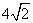 C.
C.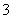 D.
D.
 所示,在三棱锥
所示,在三棱锥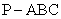 中,
中,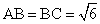 ,平面
,平面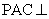 平面
平面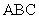 ,
,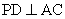 于点
于点 ,
,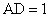 ,
,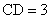 ,
,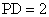 .
.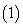 求三棱锥
求三棱锥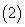 证明:
证明: 为直角三角形.
为直角三角形.