题目内容
20.点O是△ABC所在平面上一点,且满足$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,则点O为△ABC的( )| A. | 外心 | B. | 内心 | C. | 重心 | D. | 垂心 |
分析 作BD∥OC,CD∥OB,连结OD,OD与BC相交于G,可得$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{OD}$,又$\overrightarrow{OB}$+$\overrightarrow{OC}$=-$\overrightarrow{OA}$,从而可得$\overrightarrow{OD}$=-$\overrightarrow{OA}$,即AG是BC边上的中线,同理可证BO,CO的延长线也为△ABC的中线,即O为三角形ABC的重心.
解答 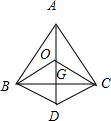 解:作BD∥OC,CD∥OB,连结OD,OD与BC相交于G,则BG=CG,(平行四边形对角线互相平分),
解:作BD∥OC,CD∥OB,连结OD,OD与BC相交于G,则BG=CG,(平行四边形对角线互相平分),
∴$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{OD}$,
又∵$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,可得:$\overrightarrow{OB}$+$\overrightarrow{OC}$=-$\overrightarrow{OA}$,
∴$\overrightarrow{OD}$=-$\overrightarrow{OA}$,
∴A,O,G在一条直线上,可得AG是BC边上的中线,
同理:BO,CO的延长线也为△ABC的中线.
∴O为三角形ABC的重心.
故选:C.
点评 本题主要考查了向量在几何中的应用,以及向量的基本运算,同时考查了转化思想和数形结合思想,属于中档题.

练习册系列答案
相关题目
10.如图所示,在△ABC中,D为BC的中点,BP⊥DA,垂足为P,且$|{\overrightarrow{BP}}|=4$,则$\overrightarrow{BC}•\overrightarrow{BP}$=( )


| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
11.已知向量$\overrightarrow{a}$=(3,4),则与$\overrightarrow{a}$方向相同的单位向量是( )
| A. | ($\frac{4}{5}$,$\frac{3}{5}$) | B. | ($\frac{3}{5}$,$\frac{4}{5}$) | C. | (-$\frac{3}{5}$-,$\frac{4}{5}$) | D. | (4,3) |
8.若对?x,y满足x>y>m>0,都有ylnx<xlny恒成立,则m的取值范围是( )
| A. | (0,e) | B. | (0,e] | C. | [e,e2] | D. | [e,+∞) |
5.函数f(x)=$\frac{ln(x-1)}{{\sqrt{2-x}}}$的定义域为( )
| A. | (1,2) | B. | (1,2] | C. | (-∞,2] | D. | (1,+∞) |