题目内容
已知点P是曲线y=x3-10x+3上位于第二象限内的一点,且该曲线在点P处的切线斜率为2,则这条切线方程为
y=2x+19
y=2x+19
.分析:设切点为P(x0,y0),求出函数的导数,根据导数的几何意义得f′(x0)=3x02-10=2,所以得x0=-2(舍正),从而得出切点为P(-2,15).根据斜率为2,利用点斜式可得直线方程,最后化成斜截式.
解答:解:设P(x0,y0),求得函数的导数为f′(x)=3x2-10
由题意知:f′(x0)=3x02-10=2,
∴x02=4.
∴结合函数图象第二象限内的一点,得x0=-2,
∴y0=15.
∴P点的坐标为(-2,15).
直线方程为y-15=2(x+2),即y=2x+19
故答案为:y=2x+19
由题意知:f′(x0)=3x02-10=2,
∴x02=4.
∴结合函数图象第二象限内的一点,得x0=-2,
∴y0=15.
∴P点的坐标为(-2,15).
直线方程为y-15=2(x+2),即y=2x+19
故答案为:y=2x+19
点评:本题考查了导数的几何意义,以及导数的运算法则和已知切线斜率求出切点坐标,本题属于基础题.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
已知点P是曲线y=lnx上的一个动点,则点P到直线l:y=x+2的距离的最小值为( )
A、
| ||||
| B、2 | ||||
C、
| ||||
D、2
|
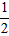 x+1
x+1