题目内容
已知圆C经过A(5,1),B(1,3)两点,圆心C在x轴上,
(1)求圆C的方程
(2)求圆C被直线lx-2y-1=0截得的弦长.
(1)求圆C的方程
(2)求圆C被直线lx-2y-1=0截得的弦长.
考点:直线与圆相交的性质
专题:计算题,直线与圆
分析:(1)根据题意可知线段AB为圆C的一条弦,根据垂径定理得到AB的垂直平分线过圆心C,所以由A和B的坐标表示出直线AB的方程,然后根据两直线垂直时斜率乘积为-1由直线AB的斜率求出AB垂直平分线的斜率,又根据中点坐标公式求出线段AB的中点坐标,由中点坐标和求出的斜率写出AB的垂直平分线的方程,又因为圆心在x轴上,所以把求出AB的垂直平分线与x轴的交点坐标即为圆心C的坐标,然后根据两点间的距离公式求出线段AC的长度即为圆的半径,根据圆心坐标和半径写出圆的标准方程即可.
(2)求出圆心到直线x-2y-1=0的距离d,代入弦长公式计算可得答案.
(2)求出圆心到直线x-2y-1=0的距离d,代入弦长公式计算可得答案.
解答:
解:(1)由A(5,1),B(1,3),
得到直线AB的方程为:y-3=
(x-1),即x+2y-7=0,
则直线AB的斜率为-
,所以线段AB的垂直平分线的斜率为2,
又设线段AB的中点为D,则D的坐标为(3,2),
所以线段AB的垂直平分线的方程为:y-2=2(x-3)即2x-y-4=0,
令y=0,解得x=2,所以线段AB的垂直平分线与x轴的交点即圆心C的坐标为(2,0),
而圆的半径r=|AC|=
,
综上,圆C的方程为:(x-2)2+y2=10.
(2)圆心到直线x-2y-1=0的距离d=
,
故所求的弦长为2
=
.
得到直线AB的方程为:y-3=
| 3-1 |
| 1-5 |
则直线AB的斜率为-
| 1 |
| 2 |
又设线段AB的中点为D,则D的坐标为(3,2),
所以线段AB的垂直平分线的方程为:y-2=2(x-3)即2x-y-4=0,
令y=0,解得x=2,所以线段AB的垂直平分线与x轴的交点即圆心C的坐标为(2,0),
而圆的半径r=|AC|=
| 10 |
综上,圆C的方程为:(x-2)2+y2=10.
(2)圆心到直线x-2y-1=0的距离d=
| 1 | ||
|
故所求的弦长为2
10-
|
14
| ||
| 5 |
点评:此题考查直线与圆的位置关系,涉及圆的弦长的求解,考查学生掌握两直线垂直时斜率满足的关系,灵活运用中点坐标公式及两点间的距离公式化简求值,掌握垂径定理的灵活运用,会根据圆心和半径写出圆的标准方程,是一道中档题.

练习册系列答案
相关题目
若a=sin(cosπx),b=cos(sinπx)且x∈[-
,-1],则( )
| 3 |
| 2 |
| A、a2+b2=1 |
| B、a<b |
| C、a>b |
| D、a=b |
已知全集U={1,2,3,4,5,6},集合A={1,3,5},B={1,2},∁U(A∪B)等于(
| A、{4} | B、{6} |
| C、{4,6} | D、∅ |
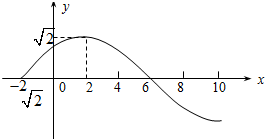 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<