题目内容
【题目】中石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分儿口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探. 由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用.勘探初期数据资料见如表:

(Ⅰ)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为![]() ,求
,求![]() ,并估计
,并估计![]() 的预报值;
的预报值;
(Ⅱ)现准备勘探新井![]() ,若通过1、3、5、7号井计算出的
,若通过1、3、5、7号井计算出的![]() 的值(
的值(![]() 精确到0.01)相比于(Ⅰ)中
精确到0.01)相比于(Ⅰ)中![]() 的值之差不超过10%,则使用位置最接近的已有旧井
的值之差不超过10%,则使用位置最接近的已有旧井![]() ,否则在新位置打开,请判断可否使用旧井?
,否则在新位置打开,请判断可否使用旧井?
(参考公式和计算结果: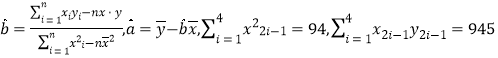 )
)
(Ⅲ)设出油量与勘探深度的比值![]() 不低于20的勘探并称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数
不低于20的勘探并称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数![]() 的分布列与数学期望.
的分布列与数学期望.
【答案】(Ⅰ) ![]() ,
, ![]() 的预报值为24; (Ⅱ)见解析; (Ⅲ)
的预报值为24; (Ⅱ)见解析; (Ⅲ) ![]() .
.
【解析】试题分析:(Ⅰ)利用前5组数据得到![]() ,由回归直线方程必过平衡点
,由回归直线方程必过平衡点![]() ,求
,求![]() ,并估计
,并估计![]() 的预报值.(Ⅱ)利用
的预报值.(Ⅱ)利用 ![]() ,均不超过
,均不超过![]() ,由此能求出结果.
,由此能求出结果.
(Ⅲ)由题意勘察优质井数![]() 的可能取值为
的可能取值为![]() ,分别求出相应的概率,由此能求出
,分别求出相应的概率,由此能求出![]() 的分布列和
的分布列和![]() .
.
试题解析:(Ⅰ)因为![]()
回归直线必过样本中心点![]() ,则
,则![]() ,
,
故回归直线方程为![]() .
.
当![]() 时,
时,![]() ,即
,即![]() 的预报值为24.
的预报值为24.
(Ⅱ)因为![]()
![]() 所以
所以
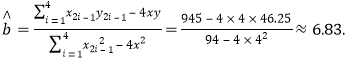
![]()
即![]() ,
,![]() .
.
![]() ,
,![]() ,均不超过
,均不超过![]() ,
,
因此使用位置最接近的已有旧井![]() .
.
(Ⅲ) 由题意,1、3、5、6这4口井是优质井,2,4这两口井是非优质井,
∴勘察优质井数![]() 的可能取值为2,3,4,
的可能取值为2,3,4,
![]() ,
,![]() ,
,![]() .
.
| 2 | 3 | 4 |
| |
|
|
![]() .
.

【题目】计划在某水库建一座至多安装![]() 台发电机的水电站,过去
台发电机的水电站,过去![]() 年的水文资料显示,水库年入流量
年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足![]() 的年份有
的年份有![]() 年,不低于
年,不低于![]() 且不超过
且不超过![]() 的年份有
的年份有![]() 年,超过
年,超过![]() 的年份有
的年份有![]() 年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(1)求未来![]() 年中,设
年中,设![]() 表示流量超过
表示流量超过![]() 的年数,求
的年数,求![]() 的分布列及期望;
的分布列及期望;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 |
|
|
|
若某台发电机运行,则该台年利润为![]() 万元,若某台发电机未运行,则该台年亏损
万元,若某台发电机未运行,则该台年亏损![]() 万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在![]()
之外的零件数,求![]() ;
;
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
, 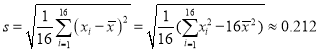 ,其中
,其中![]() 为抽取的第
为抽取的第![]() 个零件的尺寸,
个零件的尺寸, ![]() .
.
用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计![]() 和
和![]() (精确到0.01).
(精确到0.01).
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
