题目内容
19.求曲线y=3x在点(1,3)处的切线方程.分析 求出原函数的导函数,得到函数在x=1时的导数,然后代入直线方程的点斜式得答案.
解答 解:由y=3x,得y′=3xln3,
∴y′|x=1=3ln3,
则曲线y=3x在点(1,3)处的切线方程为y-3=3ln3(x-1),
即(3ln3)x-y-3ln3+3=0.
点评 本题考查利用导数研究过曲线上某点处的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,是中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
7.函数f(x)=$\frac{{2}^{x}+1}{{2}^{x}-1}$是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
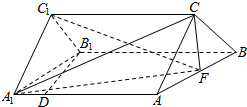 已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,△ABC为边长为1的正三角形,且AA1=2,D为AA1上的点,且A1D=$\frac{1}{4}$,F为AB的中点.
已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,△ABC为边长为1的正三角形,且AA1=2,D为AA1上的点,且A1D=$\frac{1}{4}$,F为AB的中点.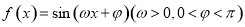 ,直线
,直线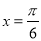 是它的一条对称轴,且
是它的一条对称轴,且 是离该轴最近的一个对称中心,则
是离该轴最近的一个对称中心,则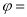 ( )
( )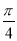 B.
B.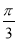 C.
C.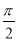 D.
D.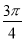
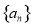 的前
的前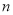 项和为
项和为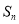 ,且
,且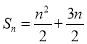 .
.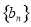 满足
满足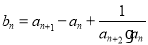 ,且数列
,且数列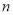 项和为
项和为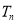 ,求证:
,求证: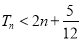 .
. ,
, ,
, .
. ,求证:
,求证: ;
; ,若
,若 ,求
,求 的值.
的值.