题目内容
1．已知函数$f（x）={e^x}-\frac{1}{2}{x^2}-mx$有极值点，则实数m的取值范围是（ ）| A． | m≥1 | B． | m＞1 | C． | 0≤m≤1 | D． | 0＜m＜1 |
分析 求出函数的导数，问题转化为g（x）=ex和h（x）=x+m有2个不同的交点，求出临界值即可．
解答 解：f′（x）=ex-x-m，
若函数f（x）有极值，
则f′（x）有零点，
即g（x）=ex和h（x）=x+m有2个不同的交点，
g（x）的切线与h（x）平行，设切点是（x0，${e}^{{x}_{0}}$），
则切线斜率是：k=${e}^{{x}_{0}}$=1，故x0=0，
故切线方程是：y=x+1，
g（x）=ex和h（x）=x+m有2个不同的交点，
则m＞1，
故选：B．
点评 不同考查了函数的单调性、极值问题，考查导数的应用以及转化思想，是一道中档题．
练习册系列答案
相关题目
12．
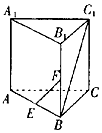如图所示，在直三棱柱ABC-A1B1C1中，AB=AA1=2，∠ABC=90°，点E、F分别是棱AB、BB1的中点，当二面角C1-AA1-B为45o时，直线EF和BC1所成的角为（ ）
如图所示，在直三棱柱ABC-A1B1C1中，AB=AA1=2，∠ABC=90°，点E、F分别是棱AB、BB1的中点，当二面角C1-AA1-B为45o时，直线EF和BC1所成的角为（ ）| A． | 45o | B． | 60o | C． | 90o | D． | 120o |
9．将4个不同的小球放入3个不同的盒子，其中有的盒子可能没有放球，则总的方法共有（ ）
| A． | 81种 | B． | 64种 | C． | 36种 | D． | 18种 |
16．下列四个命题中错误的是（ ）
| A． | 在一次试卷分析中，从每个考室中抽取第5号考生的成绩进行统计，不是简单随机抽样 | |||||||||||||||||||
| B． | 对一个样本容量为100的数据分组，各组的频数如下：
| |||||||||||||||||||
| C． | 设产品产量与产品质量之间的线性相关系数为-0.91，这说明二者存在着高度相关 | |||||||||||||||||||
| D． | 通过随机询问110名性别不同的行人，对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查，得到如表列联表：
|
13．将函数$y=sin（{2x+\frac{π}{6}}）$的图象向左平移$\frac{π}{6}$个单位，得到函数y=f（x）的图象，则下列关于函数y=f（x）的说法正确的是（ ）
| A． | 奇函数 | B． | 周期是$\frac{π}{2}$ | ||
| C． | 关于直线$x=\frac{π}{12}$对称 | D． | 关于点$（{-\frac{π}{4}，0}）$对称 |
10．已知函数f（x）=$\frac{1}{2}$x4-2x3+3m（x∈R），若f（x）+6≥0恒成立，则实数m的取值范围是（ ）
| A． | m≥$\frac{5}{2}$ | B． | m＞$\frac{5}{2}$ | C． | m≤$\frac{5}{2}$ | D． | m＜$\frac{5}{2}$ |