题目内容
设圆C：（x-k）2+（y-2k+1）2=1，则圆C的圆心轨迹方程是 ，若直线l：3x+ty-1=0截圆C所得的弦长与k无关，则t= ．
考点：直线与圆的位置关系,轨迹方程
专题：计算题,直线与圆
分析：利用消参法，可得圆C的圆心轨迹方程，直线l：3x+ty-1=0截圆C所得的弦长与k无关，则圆心到直线的距离为定值，可得直线l：3x+ty-1=0与y=2x-1平行，即可求出t的值．
解答：
解：设圆心C（x，y），则x=k，y=2k-1，
消去k可得y=2x-1；
直线l：3x+ty-1=0截圆C所得的弦长与k无关，则圆心到直线的距离为定值，
∴直线l：3x+ty-1=0与y=2x-1平行，
∴-
=2，
∴t=-
．
故答案为：y=2x-1；-
．
消去k可得y=2x-1；
直线l：3x+ty-1=0截圆C所得的弦长与k无关，则圆心到直线的距离为定值，
∴直线l：3x+ty-1=0与y=2x-1平行，
∴-
| 3 |
| t |
∴t=-
| 3 |
| 2 |
故答案为：y=2x-1；-
| 3 |
| 2 |
点评：本题考查轨迹方程，考查直线与圆的位置关系，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
程序框图如下：
如果上述程序运行结果S的值比2015小，且使输出的S最大，那么判断框中应填入（ ）
如果上述程序运行结果S的值比2015小，且使输出的S最大，那么判断框中应填入（ ）
| A、k≤10 | B、k≥10 |
| C、k≤9 | D、k≥9 |
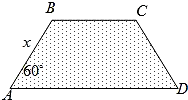某地区要建造一条防洪堤，其横断面为等腰梯形（如图），考虑到防洪堤坚固性及石块用料等因素，设计其横断面要求面积为9| 3 |
| 3 |
| A、[3，5] |
| B、（3，5） |
| C、（2，6] |
| D、[2，6） |