题目内容
已知△ABC中,点D在BC边上,且| CD |
| DB |
| CD |
| AB |
| AC |
分析:根据点D是BC边上的一个三等分点,靠近B点,得到
与
之间的关系,根据向量减法的法则,写出
与三角形的另外两条边之间的关系,得到要求的值.
| CD |
| CB |
| CB |
解答:解:∵
=2
,
∴
=
=
(
-
)
=
-
∵
=r
+s
,
∴r=
,s=-
∴r+s=0,
故答案为:0
| CD |
| DB |
∴
| CD |
| 2 |
| 3 |
| CB |
| 2 |
| 3 |
| AB |
| AC |
=
| 2 |
| 3 |
| AB |
| 2 |
| 3 |
| AC |
∵
| CD |
| AB |
| AC |
∴r=
| 2 |
| 3 |
| 2 |
| 3 |
∴r+s=0,
故答案为:0
点评:本题考查平面向量的基本定理,考查向量的加减的运算的三角形法则,是一个基础题,这种题目运算量不大,但是要注意向量的方向容易出错.

练习册系列答案
相关题目
已知△ABC中,点D在BC边上,且
=2
,
=r
+s
,则r+s的值是( )
| CD |
| DB |
| CD |
| AB |
| AC |
A、
| ||
B、
| ||
| C、-3 | ||
| D、0 |
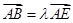
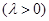 ,
,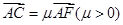 ,则
,则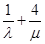 的最小值是
.
的最小值是
.