题目内容
已知△ABC中，点D是BC的中点，过点D的直线分别交直线AB、AC于E、F两点，若
=λ
（λ＞0），
=μ
(μ＞0)，则
+
的最小值是
．
| AB |
| AE |
| AC |
| AF |
| 1 |
| λ |
| 4 |
| μ |
| 9 |
| 2 |
| 9 |
| 2 |
分析：由题意可得
=
+
，由D、E、F三点共直线可得
+
=1，故
+
=（
+
）（
+
）=
+
+
，下面由基本不等式可得答案．
| AD |
| λ |
| 2 |
| AE |
| μ |
| 2 |
| AF |
| λ |
| 2 |
| μ |
| 2 |
| 1 |
| λ |
| 4 |
| μ |
| 1 |
| λ |
| 4 |
| μ |
| λ |
| 2 |
| μ |
| 2 |
| 5 |
| 2 |
| 2λ |
| μ |
| μ |
| 2λ |
解答：解：由题意可得
+
=2
，即λ
+μ
=2
，
故
=
+
，由D、E、F在同一条直线上，故
+
=1
所以
+
=（
+
）（
+
）=
+
+
因为λ＞0，μ＞0由基本不等式可得
+
+
≥
+2
=
当且仅当
=
，即μ=2λ时取等号．
故答案为：
| AB |
| AC |
| AD |
| AE |
| AF |
| AD |
故
| AD |
| λ |
| 2 |
| AE |
| μ |
| 2 |
| AF |
| λ |
| 2 |
| μ |
| 2 |
所以
| 1 |
| λ |
| 4 |
| μ |
| 1 |
| λ |
| 4 |
| μ |
| λ |
| 2 |
| μ |
| 2 |
| 5 |
| 2 |
| 2λ |
| μ |
| μ |
| 2λ |
因为λ＞0，μ＞0由基本不等式可得
| 5 |
| 2 |
| 2λ |
| μ |
| μ |
| 2λ |
| 5 |
| 2 |
|
| 9 |
| 2 |
当且仅当
| 2λ |
| μ |
| μ |
| 2λ |
故答案为：
| 9 |
| 2 |
点评：本题为向量与基本不等式的结合，其中向量式的结论和“1”的代入是解决问题的关键，属基础题．
练习册系列答案
相关题目
已知△ABC中，点D在BC边上，且
=2
，
=r
+s
，则r+s的值是（ ）
| CD |
| DB |
| CD |
| AB |
| AC |
A、
| ||
B、
| ||
| C、-3 | ||
| D、0 |
，若
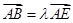
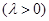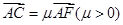,则r+s的值是( )
B.0 C.
D.-3
，
，则
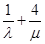的最小值是
．