题目内容
（2013•丽水一模）若两个非零向量
，
满足|
+
|=|
-
|=2|
|，则向量
与
+
的夹角是
．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| a |
| b |
| π |
| 3 |
| π |
| 3 |
分析：将|
+
|=|
-
|=2|
|平方，转化可得
•
=0，
2=3
2，令
=
，
=
，
=
+
=
+
，数形结合求得cos∠BOC 的值，可得∠BOC 的值，即为所求．
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
| a |
| OA |
| a |
| OB |
| b |
| OC |
| OA |
| OB |
| a |
| b |
解答：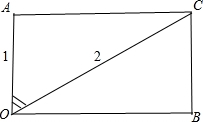
解：由已知得
．化简①得
•
=0，再化简②可得
2=3
2．
令
=
，
=
，
=
+
=
+
，则由
•
=0以及
2=3
2，可得四边形OACB为矩形，∠AOC即为向量
与
+
的夹角．
令OA=1，则OC=2，直角三角形OBC中，cos∠BOC=
=
，
∴∠AOC=
，
故答案为
．
解：由已知得
|
| a |
| b |
| b |
| a |
令
| OA |
| a |
| OB |
| b |
| OC |
| OA |
| OB |
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| a |
| b |
令OA=1，则OC=2，直角三角形OBC中，cos∠BOC=
| OA |
| OC |
| 1 |
| 2 |
∴∠AOC=
| π |
| 3 |
故答案为
| π |
| 3 |
点评：本题考查向量的数量积、模、夹角的运算．本题的关键是将已知转化，得出
、
的关系，属于中档题．
| a |
| b |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
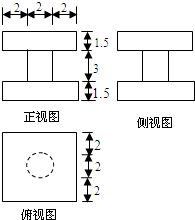（2013•丽水一模）某几何体的三视图如图所示，则该几何体的体积为
（2013•丽水一模）已知抛物线的顶点在坐标原点，焦点在y轴上，且过点（2，1），