题目内容
7.设x,y满足约束条件$\left\{\begin{array}{l}{2x-y+2≥0}\\{8x-y-4≤0}\\{x≥0,y≥0}\end{array}\right.$,若目标函数z=abx+y(a>0,b>0)的最大值为18,则2a+b的最小值为( )| A. | 4 | B. | 2$\sqrt{7}$ | C. | 4$\sqrt{7}$ | D. | 4$\sqrt{14}$ |
分析 作可行域,平移目标直线可得直线过点B(1,4)时,目标函数取最大值,可得ab=16,由基本不等式可得.
解答 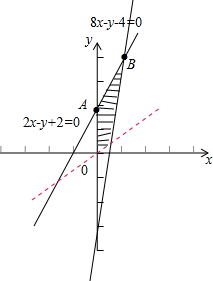 解:作出约束条件$\left\{\begin{array}{l}{2x-y+2≥0}\\{8x-y-4≤0}\\{x≥0,y≥0}\end{array}\right.$,所对应的可行域,(如图阴影)
解:作出约束条件$\left\{\begin{array}{l}{2x-y+2≥0}\\{8x-y-4≤0}\\{x≥0,y≥0}\end{array}\right.$,所对应的可行域,(如图阴影)
变形目标函数可得y=abx-z,其中a>0,b>0,
经平移直线y=abx可知,当直线经过点A(0,2)或B(1,4)时,
目标函数取最大值,显然A不合题意,
∴ab+4=18,即ab=14,
由基本不等式可得2a+b≥2$\sqrt{2ab}$=4$\sqrt{7}$,当且仅当2a=b=2$\sqrt{7}$时取等号,
故选:C.
点评 本题考查线性规划,涉及基本不等式的应用和分类讨论的思想,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列四组函数中,表示同一函数的是( )
| A. | f(x)=x0与g(x)=1 | B. | f(x)=x与g(x)=$\frac{{x}^{2}}{x}$ | ||
| C. | f(x)=x2-1与g(x)=x2+1 | D. | f(x)=|x|与g(x)=$\sqrt{{x}^{2}}$ |
15.在等差数列{an}中,若a5,a7是方程x2-2x-6=0的两根,则{an}的前11项的和为( )
| A. | 22 | B. | -33 | C. | -11 | D. | 11 |
2.等比数列{an}中,a2=4,a6和a2的等比中项等于±6,则a6=( )
| A. | 9 | B. | -9 | C. | ±8 | D. | 8 |
16.将函数y=sinπx的图象沿x轴伸长到横坐标为原来的2倍,再向左平移1个单位,得到的图象对应的解析式是( )
| A. | $y=sin(\frac{πx}{2}+1)$ | B. | y=sin(2πx+1) | C. | $y=cos\frac{πx}{2}$ | D. | $y=-cos\frac{πx}{2}$ |