题目内容
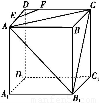
如图所示,正方体ABCD
A1B1C1D1的棱长为6,则以正方体ABCDA1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球,所得的圆为底面的圆锥的全面积为 .
【答案】
(18
+24)π
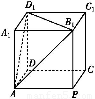
【解析】设O为正方体外接球的球心,
则O也是正方体的中心,
正三角形AB1D1的边长为6,
其外接圆的半径为
×
×6=2
.
又球的半径是正方体对角线长的一半,
即圆锥的母线长为3
,
因此圆锥底面面积为S1=π·(2)2=24π,
圆锥的侧面积为S2=π×2×3=18π.
∴S圆锥表=S1+S2=18π+24π=(18+24)π.
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
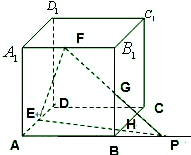如图所示，在正方体ABCD-A1B1C1D1中，其边长为2，E、F分别是AD，A1B1的中点，G、H是BB1，BC的两个动点，
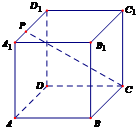如图所示，已知点P是正方体ABCD-A1B1C1D1的棱A1D1上的一个动点，设异面直线AB与CP所成的角为α，则cosα的最小值是
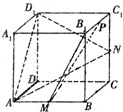如图所示，在正方体ABCD-A1B1C1D1中，AB=2，M、N分别是AB、CC1的中点，三角形MB1P的顶点P在棱C1B1上运动，给出下列结论：
