题目内容
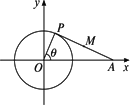
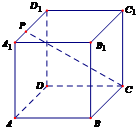如图所示，已知点P是正方体ABCD-A1B1C1D1的棱A1D1上的一个动点，设异面直线AB与CP所成的角为α，则cosα的最小值是分析：建立空间直角坐标系，可得cosα=|cos＜
，
＞|，由函数的最值可得答案．
| AB |
| CP |
解答：解：以D为坐标原点，DA，DC，DD1分别为x、y、z轴建立空间直角坐标系，
设正方体的棱长为1，则A（1，0，0），B（1，1，0），C（0，1，0），P（x，0，1），其中0≤x≤1，
∴
=（0，1，0），
=（x，-1，1），
∴cosα=|cos＜
，
＞|=
，
可知当x=1，即P与A1重合时，cosα=
取最小值
．
故答案为：
设正方体的棱长为1，则A（1，0，0），B（1，1，0），C（0，1，0），P（x，0，1），其中0≤x≤1，
∴
| AB |
| CP |
∴cosα=|cos＜
| AB |
| CP |
| 1 | ||
|
可知当x=1，即P与A1重合时，cosα=
| 1 | ||
|
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考查异面直线所成的角，涉及函数的最值得求解，建立坐标系是解决问题的关键，属中档题．
练习册系列答案
相关题目
