题目内容
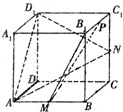 如图所示,在正方体ABCD-A1B1C1D1中,AB=2,M、N分别是AB、CC1的中点,三角形MB1P的顶点P在棱C1B1上运动,给出下列结论:
如图所示,在正方体ABCD-A1B1C1D1中,AB=2,M、N分别是AB、CC1的中点,三角形MB1P的顶点P在棱C1B1上运动,给出下列结论:①异面直线B1M与DC所成的角为π-arctan2;
②平面MB1P⊥平面ND1A;
③点A1到平面MB1P的距离等于
4
| ||
| 5 |
④三角形MB1P在平面ABCD内的射影面积为定值.
其中正确的有
分析:异面直线B1M与DC所成的角为∠B1MB,由tan∠B1MB=
=2,知异面直线B1M与DC所成的角为arctan2;平面MB1P⊥平面ND1A不成立;连接A1M,作A1E⊥B1M,交BM于E,由A1E⊥B1M,A1E⊥B1P,B1M∩B1P=B1,故点A1到平面MB1P的距离等于线段A1E.由S△MB1P=
×2×2=
×
×A1E,解得A1E=
=
;三角形MB1P在平面ABCD内的射影面积不为定值.
| B1B |
| MB |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 | ||
|
4
| ||
| 5 |
解答:解:异面直线B1M与DC所成的角为∠B1MB,
∵tan∠B1MB=
=2,
∴异面直线B1M与DC所成的角为arctan2,故①不正确;
平面MB1P⊥平面ND1A不成立,故②不正确;
连接A1M,作A1E⊥B1M,交BM于E,
∵A1E⊥B1M,A1E⊥B1P,B1M∩B1P=B1,
∴A1E⊥平面MB1P,∴点A1到平面MB1P的距离等于线段A1E.
∵AB=2,M是AB中点,
∴A1M=B1M=
,
S△MB1P=
×2×2=
×
×A1E,
解得A1E=
=
,故③正确;
三角形MB1P在平面ABCD内的射影面积不为定值,故④不正确.
故答案为:③.
∵tan∠B1MB=
| B1B |
| MB |
∴异面直线B1M与DC所成的角为arctan2,故①不正确;
平面MB1P⊥平面ND1A不成立,故②不正确;
连接A1M,作A1E⊥B1M,交BM于E,
∵A1E⊥B1M,A1E⊥B1P,B1M∩B1P=B1,
∴A1E⊥平面MB1P,∴点A1到平面MB1P的距离等于线段A1E.
∵AB=2,M是AB中点,
∴A1M=B1M=
| 5 |
S△MB1P=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
解得A1E=
| 4 | ||
|
4
| ||
| 5 |
三角形MB1P在平面ABCD内的射影面积不为定值,故④不正确.
故答案为:③.
点评:本题考查命题的真假判断,具体涉及到异面直线所成的角、平面与平面垂直、点到直线的距离、射影面积等基本知识点,解题时要认真审题,注意空间想象力的培养.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
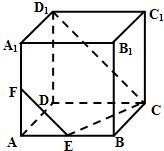 如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点
如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点
 (2011•宝山区二模)如图所示,在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等,则动点P所在曲线形状为( )
(2011•宝山区二模)如图所示,在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等,则动点P所在曲线形状为( ) 如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等,则动点P所在曲线的形状为( )
如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等,则动点P所在曲线的形状为( )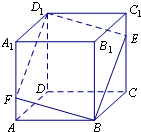 如图所示,在正方体ABCD-A1B1C1D1中,点E是棱CC1上的一个动点,平面BED1交棱AA1于点F.则下列命题中假命题是( )
如图所示,在正方体ABCD-A1B1C1D1中,点E是棱CC1上的一个动点,平面BED1交棱AA1于点F.则下列命题中假命题是( )