题目内容
8.已知函数f(x)=(x2+x)(x2+ax+b),若对?x∈R,均有f(x)=f(2-x),则f(x)的最小值为-$\frac{9}{4}$.分析 由f(0)=f(2),f(-1)=f(3)可求得a,b,从而确定函数f(x),从而求导确定函数的极值,从而求最小值.
解答 解:∵对?x∈R,均有f(x)=f(2-x),
∴f(0)=f(2),f(-1)=f(3),
即0=6(4+2a+b),0=12(9+3a+b),
解得,a=-5,b=6;
故f(x)=(x2+x)(x2-5x+6),
令f′(x)=(2x+1)(x2-5x+6)+(x2+x)(2x-5)
=(x-1)(2x2-4x-3)=0,
解得,x=1或x=1+$\frac{\sqrt{10}}{2}$或x=1-$\frac{\sqrt{10}}{2}$;
由函数的对称性知,
当x=1+$\frac{\sqrt{10}}{2}$或x=1-$\frac{\sqrt{10}}{2}$时,函数f(x)都可以取到最小值,
f(1+$\frac{\sqrt{10}}{2}$)=-$\frac{9}{4}$,
故答案为:-$\frac{9}{4}$.
点评 本题考查了导数的综合应用及学生的化简运算能力,属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
5.已知函数$f(x)=2{sin^2}(x+\frac{π}{4})$,则下列结论正确的是( )
| A. | f(x)是奇函数 | B. | x=$-\frac{π}{4}$是f(x)一条对称轴 | ||
| C. | f(x)的最小正周期为$\frac{π}{2}$ | D. | ($-\frac{π}{4}$,0)是f(x)的一条对称轴 |
9.在区间(0,3]上随机取一个数x,则事件“-1≤x≤$\frac{1}{2}$”发生的概率为( )
| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
10.设f(x)=ax2+bx+2是定义在[1+a,1]上的偶函数,则f(x)>0的解集为( )
| A. | (-2,2) | B. | ∅ | C. | (-∞,-1)∪(1,+∞) | D. | (-1,1) |

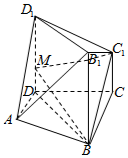 如图,几何体ABCD-B1C1D1中,正方形BB1D1D⊥平面ABCD,D1D∥CC1,平面D1DCC1与平面B1BCC1所成的二面角的余弦值为$\frac{2}{3}$,BC=3,CD=2CC1=2,AD=$\sqrt{5}$,AD∥BC,M为DD1上任意一点.
如图,几何体ABCD-B1C1D1中,正方形BB1D1D⊥平面ABCD,D1D∥CC1,平面D1DCC1与平面B1BCC1所成的二面角的余弦值为$\frac{2}{3}$,BC=3,CD=2CC1=2,AD=$\sqrt{5}$,AD∥BC,M为DD1上任意一点.