题目内容
已知0＜α＜
，tan
=
，求值：（1）tanα（2）cos（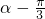
）
解：（1）∵0＜α＜，tan=，∴tanα=
=
． …6′
（2）由tanα=，可得 
，…10′
∴
=cosαcos
+sinα sin=
+
=
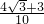． …14′
分析：（1）利用二倍角公式可得 tanα=，把tan=代入运算求得结果．
（2）由tanα=，可得 ，利用两角差的余弦公式求得 的值．
点评：本题考查二倍角公式，同角三角函数的基本关系，两角差的余弦公式的应用，求出，是解题的
关键．
，tan=，∴tanα==． …6′（2）由tanα=
，可得 ，…10′∴
=cosαcos+sinα sin=+=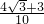． …14′分析：（1）利用二倍角公式可得 tanα=
，把tan=代入运算求得结果．（2）由tanα=
，可得 ，利用两角差的余弦公式求得 的值．点评：本题考查二倍角公式，同角三角函数的基本关系，两角差的余弦公式的应用，求出
，是解题的关键．
练习册系列答案
相关题目
<
<
<
,tan
=
,cos(
.