Question

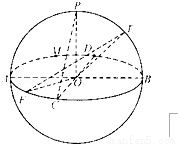
（2011•成都二模）如图，在半径为l的球O中．AB、CD是两条互相垂直的直径，半径OP⊥平面ACBD．点E、F分别为大圆上的劣弧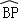、的中点，给出下列结论：

①E、F两点的球面距离为；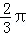

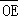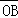②向量在向量方向上的投影恰为；

③若点M为大圆上的劣弧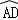的中点，则过点M且与直线EF、PC成等角的直线有无数条；

④球面上到E、F两点等距离的点的轨迹是两个点；

其中你认为正确的所有结论的序号为 ．

Answer 1

①③

【解析】

试题分析：先建立如图所示的空间直角坐标系，写出坐标E（0，，），F（，﹣，0）B（0，1，0），P（0，0，1）C（1，0，0）再一一验证即可．

【解析】
建立如图所示的空间直角坐标系，则E（0，，），F（，﹣，0）B（0，1，0），P（0，0，1）C（1，0，0）①cos∠EOF=cos∠EOBcos∠COB=cos45°cos（90°+45°）=﹣=﹣∴，对；

②向量在向量方向上的投影为，错；

③由于等角的值不是一定值，因此将直线EF、PC都平移到点M，可知过点M且与直线EF、PC成等角的直线有无数多条，对；

④过点EF的中点及球心O的大圆上任意点到点E、F的距离都相等，错；

故答案为①③