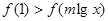题目内容
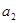 ,
,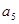 是方程
是方程
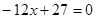 的两根, 数列
的两根, 数列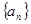 是公差为正的等差数列,数列
是公差为正的等差数列,数列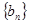 的前
的前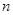 项和为
项和为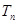 ,且
,且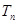
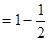
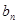
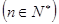 .
.
(1)求数列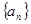 ,
,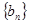 的通项公式;
的通项公式;
(2)记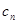 =
=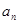
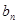 ,求数列
,求数列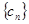 的前
的前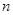 项和
项和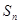 .
.
(1) ,
, (3)
(3)
解析试题分析:解:(1)由 .且
.且 得
得
 ,
,

在 中,令
中,令 得
得 当
当 时,T
时,T =
=
 ,
,
两式相减得 ,
,
 .
.
(2) ,
,  ,
, ,
, =2
=2
= ,
, 
考点:等差数列和数列的求和
点评:解决该试题的关键是能利用等差数列的连个基本量表示得到其通项公式,同时得到两个数列的通项公式,同时结合错位相减法来求和,属于中档题。

练习册系列答案
相关题目
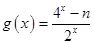 是奇函数,
是奇函数,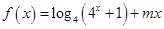 是偶函数。(1)求
是偶函数。(1)求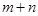 的值;(2)设
的值;(2)设 若
若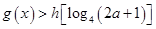 对任意
对任意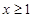 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。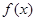 是定义在
是定义在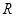 上的偶函数,且
上的偶函数,且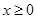 时,
时, 。
。 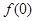 ,
,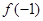 ;
;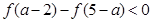 ,求
,求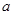 的取值范围。
的取值范围。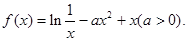
 是定义域上的单调函数,求
是定义域上的单调函数,求 的取值范围;
的取值范围;
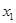 、
、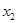 ,证明:
,证明: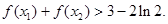
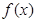 是定义在
是定义在 上的偶函数,已知当
上的偶函数,已知当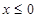 时,
时,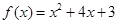 .
.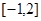 上的值域。
上的值域。 ,其中e是自然数的底数,
,其中e是自然数的底数, .
.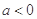 时,解不等式
时,解不等式 ;
;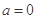 时,求正整数k的值,使方程
时,求正整数k的值,使方程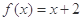 在[k,k+1]上有解;
在[k,k+1]上有解;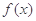 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求 的取值范围.
的取值范围. 是定义在
是定义在 上的偶函数,当
上的偶函数,当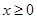 时,
时,
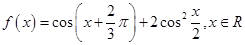 。
。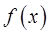 的值域;
的值域;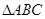 的内角A、B、C的对边长分别为a,b,c,若
的内角A、B、C的对边长分别为a,b,c,若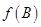 =1,b=1,c=
=1,b=1,c=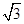 ,求a的值。
,求a的值。 ,若
,若 为定义在R上的奇函数,则(1)求实数
为定义在R上的奇函数,则(1)求实数 的值;(2)求函数
的值;(2)求函数 的不等式:
的不等式: