题目内容
(本小题12分)
已知函数 是定义在
是定义在 上的偶函数,当
上的偶函数,当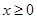 时,
时,
(1)求函数 的解析式,并画出函数
的解析式,并画出函数 的图像。
的图像。
(2)根据图像写出的单调区间和值域。
(1) 
(2) 函数 的单调递增区间为
的单调递增区间为
单调递减区间为 ,函数
,函数 的值域为
的值域为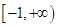 —
—
解析试题分析:解:(1)由 ,当
,当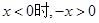 ,
,
又函数 为偶函数,
为偶函数,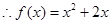 —————————————3’
—————————————3’
故函数的解析式为 —————————————4’
—————————————4’
(2)由函数的图像可知,函数 的单调递增区间为
的单调递增区间为
单调递减区间为 ,函数
,函数 的值域为
的值域为 ——————12’
——————12’
考点:函数奇偶性和函数单调性的运用
点评:解决该试题的关键是利用对称性作图,并能加以结合单调性的性质来求解最值。属于基础题。

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 ,
, ,且
,且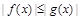 对
对 恒成立.
恒成立. ,不等式
,不等式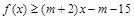 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. ,那么当
,那么当 时,是否存在区间
时,是否存在区间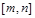 (
( ),使得函数
),使得函数 在区间
在区间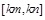 ?若存在,请求出区间
?若存在,请求出区间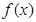 和
和 的图象关于原点对称,且
的图象关于原点对称,且 .
.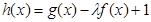 在[-1,1]上是增函数,求实数
在[-1,1]上是增函数,求实数 的取值范围
的取值范围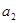 ,
,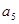 是方程
是方程
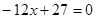 的两根, 数列
的两根, 数列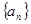 是公差为正的等差数列,数列
是公差为正的等差数列,数列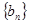 的前
的前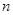 项和为
项和为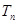 ,且
,且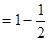
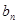
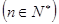 .
.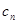 =
=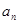
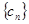 的前
的前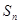 .
. .
. 在区间
在区间 上是增函数还是减函数?证明你的结论;
上是增函数还是减函数?证明你的结论; 时,
时, 恒成立,求整数
恒成立,求整数 的最大值;
的最大值; (
( )。
)。 是定义在R上的奇函数,当
是定义在R上的奇函数,当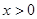 时,
时,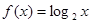
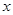 的不等式
的不等式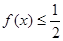

 .
. 时①求
时①求 的单调区间;
的单调区间;  ,若对任意
,若对任意 ,存在
,存在 ,使
,使 ,求实数
,求实数 取值范围.
取值范围. 时,恒有
时,恒有 成立,求
成立,求 的取值范围.
的取值范围.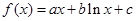 ,
,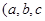 是常数)在x=e处的切线方程为
是常数)在x=e处的切线方程为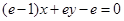 ,
, 既是函数
既是函数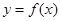 的零点,又是它的极值点.
的零点,又是它的极值点. 在区间(1,3)内不是单调函数,求实数m的取值范围;
在区间(1,3)内不是单调函数,求实数m的取值范围;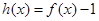 的单调递减区间,并证明:
的单调递减区间,并证明: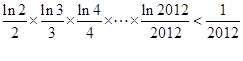
 对于任意实数
对于任意实数 满足
满足 ,当
,当 时,
时, .
. 并判断
并判断 ,集合
,集合 ,
, ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.