题目内容
已知函数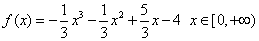 。
。
⑴求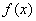 的极值;
的极值;
⑵当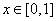 时,求
时,求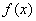 的值域;
的值域;
⑶设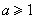 ,函数
,函数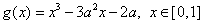 ,若对于任意
,若对于任意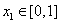 ,总存在
,总存在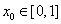 ,使得
,使得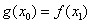 成立,求
成立,求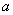 的取值范围。
的取值范围。
解:⑴ ,令
,令 ,解得:
,解得: (舍)或
(舍)或
当 时,
时, ;当
;当 时,
时, ,
,

 ,无极小值.
,无极小值.
⑵由⑴知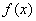 在区间
在区间 单调递增,
单调递增,
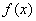 在区间
在区间 的值域为
的值域为 ,即
,即 .
.
⑶
 且
且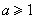 ,
, 当
当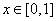 时
时 ,
,
 在区间
在区间 单调递减,
单调递减,
 在区间
在区间 的值域为
的值域为 ,即
,即 .
.
又对于任意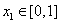 ,总存在
,总存在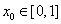 ,使得
,使得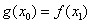 成立
成立
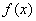 在区间
在区间 的值域
的值域
 在区间
在区间 的值域,即
的值域,即

 ,
,
 ,解得:
,解得: .
.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 ,则
,则 是
是 的( )条件.
的( )条件.
 在
在 上单调递减,则实数
上单调递减,则实数 的取值范围为( )
的取值范围为( ) B.
B.  C.
C. D.
D. 
 (
( )
) 是实数,求
是实数,求 的值;
的值; 内,
内, 为了了解高三学生的身体状况,抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图)。已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则抽取的男生人数是 .
为了了解高三学生的身体状况,抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图)。已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则抽取的男生人数是 . 为等差数列,首项
为等差数列,首项 ,公差
,公差 ,若
,若 成等比数列,且
成等比数列,且 ,
, ,
, ,则数列
,则数列 的通项公式
的通项公式 .
. 的各项均为正数,对
的各项均为正数,对 ,
, ,
, ,则
,则
 B.
B. C.
C. D.
D.