题目内容
设A、B分别为椭圆(1)求椭圆的方程;
(2)设P为右准线上不同于点(4,0)的任意一点,若直线AP、BP分别与椭圆相交于异于A、B的点M、N,证明点B在以MN为直径的圆内.
解:(1)依题意得 a=2c,![]() =4,解得a=2,c=1,从而b=
=4,解得a=2,c=1,从而b=![]() .
.
故椭圆的方程为![]() =1.
=1.
(2)解法1:由(1)得A(-2,0),B(2,0).设M(x0,y0).
∵M点在椭圆上,∴y0=![]() (4-x02).①又点M异于顶点A、B,∴-2<x0<2,
(4-x02).①又点M异于顶点A、B,∴-2<x0<2,
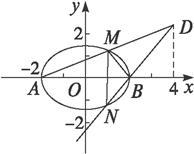
由P、A、M三点共线可以得P(4,![]() ).
).
从而![]() =(x0-2,y0),
=(x0-2,y0),![]() =(2,
=(2,![]() ).
).
∴![]() ·
·![]() =2x0-4+
=2x0-4+![]() +2=
+2=![]() (x02-4+3y02)②
(x02-4+3y02)②
将①代入②,化简得![]() ·
·![]() =
=![]() (2-x0).
(2-x0).
∵2-x0>0,∴![]() ·
·![]() >0,则∠MBP为锐角,从而∠MBN为钝角,
>0,则∠MBP为锐角,从而∠MBN为钝角,
故点B在以MN为直径的圆内.
解法2:由(1)得A(-2,0),B(2,0).
设M(x1,y1),N(x2,y2),则-2<x1<2,-2<x2<2,又MN的中点Q的坐标为(![]() ).依题意,计算点B到圆心Q的距离与半径的差
).依题意,计算点B到圆心Q的距离与半径的差
|BQ|2-![]() |MN|2=(
|MN|2=(![]() -2)2+(
-2)2+(![]() )2-
)2-![]() [(x1-x2)2+(y1-y2)2]=(x1-2)(x2-2)+y1y2 ③
[(x1-x2)2+(y1-y2)2]=(x1-2)(x2-2)+y1y2 ③
又直线AP的方程为y=![]() (x+2),直线BP的方程为y=
(x+2),直线BP的方程为y=![]() (x-2).
(x-2).
而两直线AP与BP的交点P在准线x=4上,
∴![]() ,即y2=
,即y2=![]() . ④
. ④
又点M在椭圆上,则![]() =1,即y12=
=1,即y12=![]() (4-x12). ⑤
(4-x12). ⑤
于是将④⑤代入③,
化简后可得|BQ|2-![]() |MN|2=
|MN|2=![]() (2-x1)(x2-2)<0.
(2-x1)(x2-2)<0.
从而,点B在以MN为直径的圆内.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目