题目内容
设x>0,y>0,x+y-x2y2=4,则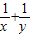 的最小值为 .
的最小值为 .
【答案】分析:将条件变形,代入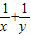 进行化简,然后利用基本不等式可求出最小值,注意等号成立的条件.
进行化简,然后利用基本不等式可求出最小值,注意等号成立的条件.
解答:解:∵x+y-x2y2=4
∴x+y=x2y2+4则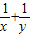 =
=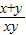 =
=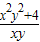 =xy+
=xy+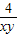 ≥2
≥2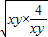 =4
=4
当且仅当xy=2时取等号
故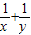 的最小值为4
的最小值为4
故答案为:4
点评:本题主要考查了基本不等式的应用,同时考查了转化的思想,属于中档题.
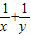 进行化简,然后利用基本不等式可求出最小值,注意等号成立的条件.
进行化简,然后利用基本不等式可求出最小值,注意等号成立的条件.解答:解:∵x+y-x2y2=4
∴x+y=x2y2+4则
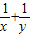 =
=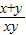 =
=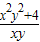 =xy+
=xy+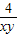 ≥2
≥2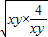 =4
=4当且仅当xy=2时取等号
故
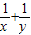 的最小值为4
的最小值为4故答案为:4
点评:本题主要考查了基本不等式的应用,同时考查了转化的思想,属于中档题.

练习册系列答案
相关题目