题目内容

(1)求函数 的解析式;
的解析式;
(2)试判断函数 在区间
在区间 上的单调性,并用函数单调性定义证明;
上的单调性,并用函数单调性定义证明;
(3)当 时,函数
时,函数 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。
(1) ;(2)单调递减;(3)
;(2)单调递减;(3)
【解析】
试题分析:(1)函数为奇函数,则 ,再用待定系数法即可求出;(2)作差法:任意的两个实数
,再用待定系数法即可求出;(2)作差法:任意的两个实数 ,证明出
,证明出 ;(3)要使
;(3)要使 则
则
试题解析:(1)








 所以
所以
(2) 由(1)问可得
由(1)问可得

 在区间(0,0.5]上是单调递减的
在区间(0,0.5]上是单调递减的
证明:设任意的两个实数



又



 ,
, 


 在区间(0,0.5]上是单调递减的;
在区间(0,0.5]上是单调递减的;
(3)由(2)知
 在区间(0,0.5]上的最小值是
在区间(0,0.5]上的最小值是
要使
则


考点:1、待定系数法;2、函数的单调性;3、不等式恒成立问题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 0.5
0.5 .若
.若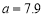 ,则
,则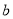 的值为
的值为 B.
B.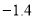 C.
C.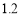 D.
D.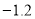
 和
和 ,成绩的标准差分别为
,成绩的标准差分别为 和
和 ,则( ).
,则( ).
 ,
,

 ,
,
 ,
,
 与曲线
与曲线
 没有公共点.若平行于
没有公共点.若平行于 的直线与曲线
的直线与曲线 有且只有一个公共点,则符合条件的直线
有且只有一个公共点,则符合条件的直线 ( ).
( ). 中随机撒一粒豆子,则豆子落在图中阴影部分的概率为( ).
中随机撒一粒豆子,则豆子落在图中阴影部分的概率为( ).
 B.
B. C.
C. D.
D.
 ;
;  ;
;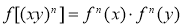 , 其中不正确的是__ .(填上所有不正确的题号)
, 其中不正确的是__ .(填上所有不正确的题号) 方程为:
方程为: ,圆
,圆 的方程为:
的方程为: ,动圆M与
,动圆M与