Question

【题目】某园林公司准备绿化一块半径为200米，圆心角为 的扇形空地（如图的扇形OPQ区域），扇形的内接矩形ABCD为一水池，其余的地方种花，若∠COP=α，矩形ABCD的面积为S（单位：平方米）．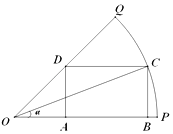
（1）试将S表示为关于α的函数，求出该函数的表达式；
（2）角α取何值时，水池的面积 S最大，并求出这个最大面积．

Answer 1

【答案】
（1）解：在Rt△OBC中，OB=200cosα，BC=200sinα

在Rt△OAD中， ，

∴OA=DA=BC=200sinα

∴AB=OB﹣OA=200cosα﹣200sinα，

故S=ABBC=（200cosα﹣200sinα）200sinα

=40000sinαcosα﹣40000sin2α=20000sin2α﹣20000（1﹣cos2α）

=20000（sin2α+cos2α）﹣20000

= ，

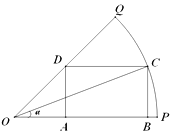
（2）解：由 ，得 ，

所以当 ，即 时，

S最大=

因此，当 时，水池的面积S最大，最大面积为 平方米

【解析】（1）在Rt△OBC中，OB=200cosα，BC=200sinα ，求出BC=200sinα，AB=200cosα﹣200sinα，得到S= ， 即可．（2）利用三角函数的最值，求解 时，水池的面积S最大，最大面积为 平方米．