Question

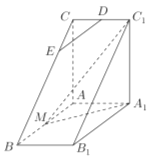
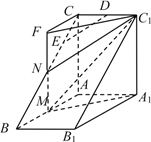
【题目】如图，直三棱柱中， ， ， 是的中点，△是等腰三角形， 为的中点， 为上一点；

（1）若∥平面，求；

（2）平面将三棱柱分成两个部分，求含有点的那部分体积；

Answer 1

【答案】(1) (2)

【解析】试题分析：(1)因为∥平面，所以找过直线ＤＥ的平面与平面的交线，进而确定所求的值。取BC的中点N，连结ＭＮ， ，根据∥∥，可得平面与平面为同一个平面，平面 平面 ，根据条件∥平面和线面平行的性质定理可得∥，再由为的中点，可得是的中点，∴．（２）含有点的那部分不是规则的几何体，体积不好求，故把该部分补成规则的几何体。延长MN至点F，使MN=NF，连结FC、FC1. 补成三棱柱所以所求部分的体积等于三棱柱的体积减去三棱锥 的体积。因为三棱柱为直三棱柱，∴平面，

又因为，所以平面，所以三棱柱是直三棱柱。

因为平面，所以 ，所以三棱锥为直三棱锥。∵，又是等腰三角形，所以. 因为BC的中点为N，所以.

试题解析：解：取中点为，连结，

∵分别为中点

∴∥∥，∴四点共面，

且平面 平面

又平面，且∥平面，∴∥

∵为的中点，∴是的中点，∴．

(2)因为三棱柱为直三棱柱，∴平面，

又，则平面。

∵，又是等腰三角形，所以.

如图，将几何体补成三棱柱

∴几何体的体积为：