题目内容
3.在等比数列{an}中,公比q=2,a1+a2=9,则a3+a4=( )| A. | 12 | B. | 18 | C. | 27 | D. | 36 |
分析 利用等比数列的通项公式即可得出.
解答 解:∵等比数列{an}中,公比q=2,a1+a2=9,
则a3+a4=q2(a1+a2)=4×9=36.
故选:D.
点评 本题考查了等比数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.下列求导数运算错误的是( )
| A. | (3x)′=3xln3 | B. | (x2lnx)′=2xlnx+x | ||
| C. | ($\frac{cosx}{x}$)′=$\frac{xsinx-cosx}{{x}^{2}}$ | D. | (x+$\frac{1}{x}$+$\sqrt{x}$)′=1-$\frac{1}{{x}^{2}}$+$\frac{1}{2\sqrt{x}}$ |
18.以下四个命题:
①“x≠2或y≠3”是“xy≠6”的充分不必要条件.
②任何一个四面体的四个侧面都不可能是直角三角形.
③若m,n是异面直线,且m⊥α,n⊥β,则α与β不会平行.
④抛物线的焦点是F(a,0)(a<0),则抛物线的标准方程是y2=4ax.
其中真命题有( )
①“x≠2或y≠3”是“xy≠6”的充分不必要条件.
②任何一个四面体的四个侧面都不可能是直角三角形.
③若m,n是异面直线,且m⊥α,n⊥β,则α与β不会平行.
④抛物线的焦点是F(a,0)(a<0),则抛物线的标准方程是y2=4ax.
其中真命题有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
8.设a>0,b>0,若$\sqrt{2}$是2a与2b的一个等比中项,则ab的最大值为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
15.已知2a+3b=2,则4a+8b的最小值为( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
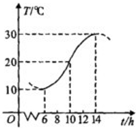 如图,某地一天从6~14时的温度变化,曲线近似满足函数y=Asin(?x+φ)+b,(A>0,?>0,φ∈(0,2π)),试求这段曲线的函数解析式.
如图,某地一天从6~14时的温度变化,曲线近似满足函数y=Asin(?x+φ)+b,(A>0,?>0,φ∈(0,2π)),试求这段曲线的函数解析式.