题目内容
9.已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=an+2n+1,数列{bn}的前n项和为Tn.
分析 (1)由题意可得Sn-1+n-1=2an-1,与条件式相减得出递推式,从而可得结论;求出{an+1}的通项即可得出{an}的通项公式;
(2)将bn分成等差数列与等比数列分别求和.
解答 解:(1)证明:令n=1得a1+1=2a1,∴a1=1,
当n≥2时,∵Sn+n=2an,∴Sn-1+n-1=2an-1,
两式相减得:an+1=2an-2an-1,即an=2an-1+1,
∴an+1=2(an-1+1)(n≥2,n∈N*),
∴数列{an+1}是以2为首项,以2为公比的等比数列.
∴an+1=2n,∴an=2n-1.
(2)bn=an+2n+1=2n+2n.
∴Tn=(2+22+23+…+2n)+2(1+2+3+…+n)=$\frac{{2({1-{2^n}})}}{1-2}+2.\frac{{({1+n})n}}{2}$=2n+1+n2+n-2.
点评 本题考查了等比数列的判定,等差数列与等比数列的前n项和公式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.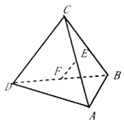 已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=6,CD=10,EF=7,则AB与CD所成角的度数为( )
已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=6,CD=10,EF=7,则AB与CD所成角的度数为( )
 已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=6,CD=10,EF=7,则AB与CD所成角的度数为( )
已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=6,CD=10,EF=7,则AB与CD所成角的度数为( )| A. | 120° | B. | 45° | C. | 60° | D. | 90° |
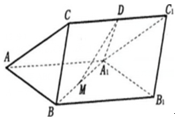 如图,三棱柱ABC-A1B1C1中,BC⊥平面ABB1A1,D,M分别为CC1和A1B的中点,△BA1B1是边长为2的正三角形,BC=1.
如图,三棱柱ABC-A1B1C1中,BC⊥平面ABB1A1,D,M分别为CC1和A1B的中点,△BA1B1是边长为2的正三角形,BC=1.




 已知直线l与椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A(a,0),B(0,b)两点,O为坐标原点,S△OAB=4,且a+b=6.
已知直线l与椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A(a,0),B(0,b)两点,O为坐标原点,S△OAB=4,且a+b=6.