题目内容
已知函数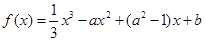 (
(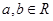 ),其图像在点(1,
),其图像在点(1,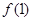 )处的切线方程为
)处的切线方程为 .
.
(1)求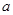 ,
,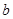 的值;
的值;
(2)求函数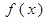 的单调区间和极值;
的单调区间和极值;
(3)求函数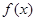 在区间[-2,5]上的最大值.
在区间[-2,5]上的最大值.
(1) 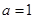 ,
,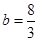 .
.
(2)函数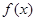 的极大值是
的极大值是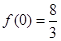 ,极小值是
,极小值是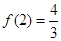 .
.
(3)函数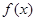 在区间
在区间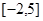 上的最大值为
上的最大值为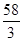 .
.
解析试题分析:(1) 由题意,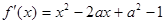 . 1分
. 1分
又∵函数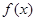 的图象在点
的图象在点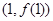 处的切线方程为
处的切线方程为 ,
,
所以切线的斜率为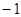 ,
,
即 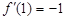 ,∴
,∴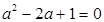 ,解得
,解得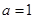 . 2分
. 2分
又∵点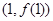 在直线
在直线 上,∴
上,∴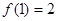 , 3分
, 3分
同时点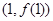 即点
即点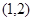 在
在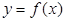 上,
上,
∴ , 4分
, 4分
即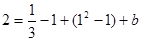 ,解得
,解得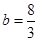 . 5分
. 5分
(2)由(1)有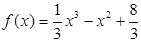 ,
,
∴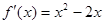 , 6分
, 6分
由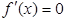 可知
可知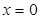 ,或
,或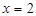 ,所以有
,所以有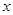 、
、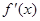 、
、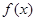 的变化情况表如下:
的变化情况表如下: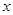
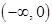
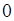
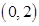
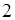
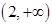
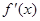
+ 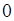
- 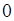
+ 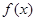
极大值 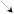
 练习册系列答案
练习册系列答案
自主假期作业本吉林大学出版社系列答案
高中新课程寒假作业系列答案
海淀黄冈寒假作业合肥工业大学出版社系列答案
寒假Happy假日系列答案
寒假成长乐园系列答案

寒假创新性自主学习寒假突破系列答案
寒假高效作业系列答案
寒假假期集训系列答案
寒假接力棒系列答案
相关题目
 (
( 为常数).
为常数).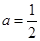 时,求
时,求 的单调递减区间;
的单调递减区间; ,且对任意的
,且对任意的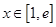 ,
, 恒成立,求实数
恒成立,求实数 ,
,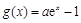 (其中
(其中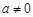 ,
,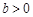 ),且函数
),且函数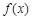 的图象在点
的图象在点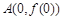 处的切线与函数
处的切线与函数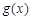 的图象在点
的图象在点 处的切线重合.
处的切线重合.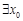 ,满足
,满足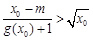 ,求实数
,求实数 的取值范围;
的取值范围;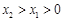 ,试探究
,试探究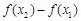 与
与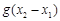 的大小,并说明你的理由.
的大小,并说明你的理由. ,
,
 ,求函数
,求函数 的极值;
的极值; ,求函数
,求函数 的单调区间;
的单调区间; (
( )上存在一点
)上存在一点 ,使得
,使得

 成立,求
成立,求 的取值范围.
的取值范围. ,
, 取得极值,求实数
取得极值,求实数 的值;
的值; 时,求
时,求 上的最小值;
上的最小值; ,直线
,直线 都不是曲线
都不是曲线 的切线,求实数
的切线,求实数 (
( 是自然对数的底数,
是自然对数的底数, ).
). 的单调区间、最大值;
的单调区间、最大值; 的方程
的方程 根的个数。
根的个数。 函数
函数
 图像以
图像以 为对称中心,求实数
为对称中心,求实数 和
和 的值
的值 ,求函数
,求函数 上的最小值
上的最小值 .
. ,试求函数
,试求函数 的单调区间;
的单调区间; 作曲线
作曲线 的切线,证明:切点的横坐标为1;
的切线,证明:切点的横坐标为1; ,若函数
,若函数 在区间(0,1]上是减函数,求
在区间(0,1]上是减函数,求 的取值范围.
的取值范围.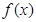 的导数
的导数 为实数,
为实数, .
. 且与曲线
且与曲线 的方程;
的方程; ,试判断函数
,试判断函数 的极值点个数。
的极值点个数。