题目内容
3.已知函数f(x)=$\sqrt{x}$;(1)求函数f(x)图象在x=1处切线l的方程;
(2)求由曲线y=$\sqrt{x}$,直线l及y轴围成图形的面积.
分析 (1)求出函数的导数,计算f(1),f′(1),求出切线方程即可;(2)求出交点坐标,根据定积分计算即可.
解答 解:(1)f′(x)=$\frac{1}{2\sqrt{x}}$,f(1)=1,f′(1)=$\frac{1}{2}$,
故切线方程是:y-1=$\frac{1}{2}$(x-1),
即$y=\frac{1}{2}x+\frac{1}{2}$;
(2)由$\left\{\begin{array}{l}{y=\frac{1}{2}(x+1)}\\{y=\sqrt{x}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,
故直线l及y轴围成图形的面积:
S=${∫}_{0}^{1}$[($\frac{1}{2}$(x+1)-$\sqrt{x}$]dx
=$\frac{1}{2}$($\frac{1}{2}$x2+x+c)${|}_{0}^{1}$-$\frac{2}{3}$${x}^{\frac{3}{2}}$${|}_{0}^{1}$
=$\frac{1}{12}$.
点评 本题考查了切线方程问题,考查导数的应用以及定积分问题,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.已知函数f(x)=x3-3x2-m存在2个零点,则这两个零点的和为( )
| A. | 1 | B. | 3 | C. | 1或4 | D. | 1或3 |
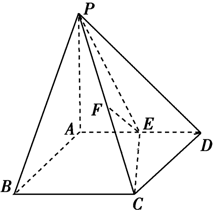 如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E、F分别为棱AD、PC的中点.
如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E、F分别为棱AD、PC的中点.