题目内容
2.△ABC是以角C为直角的等腰直角三角形,AC=2,点H位于AB边上,沿CH折叠△ABC,若折叠过程中始终有AB⊥CH,则三棱锥H-ABC的体积最大值为$\frac{\sqrt{2}}{3}$.分析 由题意画出图形,依据折叠过程中始终有AB⊥CH,可得H为AB的中点,然后利用等积法求得使多面体HABC体积取最大值时A的位置,代入三棱锥体积公式求得答案.
解答 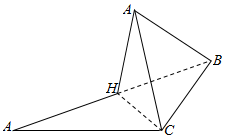 解:如图,∵△ABC是以角C为直角的等腰直角三角形,且AC=2,
解:如图,∵△ABC是以角C为直角的等腰直角三角形,且AC=2,
∴BC=2,AC=$2\sqrt{2}$,
又点H位于AB边上,且沿CH折叠△ABC的过程中始终有AB⊥CH,
即CH⊥平面ABH,∴CH⊥AB,则H为AB的中点,
∵三棱锥H-ABC的体积等于三棱锥A-BCH的体积,
∴要使三棱锥H-ABC的体积最大,则需三棱锥A-BCH的高最大,
即当AH⊥平面BCH时体积最大,
此时${S}_{△BCH}=\frac{1}{2}{S}_{△BCH}=\frac{1}{2}×\frac{1}{2}×2×2=1$,AH=$\frac{1}{2}AB=\sqrt{2}$.
∴三棱锥H-ABC的体积最大值为$\frac{1}{3}×1×\sqrt{2}=\frac{\sqrt{2}}{3}$.
故答案为:$\frac{\sqrt{2}}{3}$.
点评 本题考查棱锥体积的求法,关键是明确折叠问题在折叠前后的变量与不变量,考查空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
12.班集体搞某项活动,将全班同学分成3个不同的小组,每位同学被分到每个小组的可能性相同,则甲、乙两位同学被分到同一个小组的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
17.有7位歌手(1至7号)参加一场歌唱比赛,由550名大众评委现场投票决定歌手名次,根据年龄将大众评委分为5组,各组的人数如下:
(Ⅰ) 为了调查大众评委对7位歌手的支持状况,现用分层抽样方法从各组中抽取若干评委,其中从B组中抽取了6人.请将其余各组抽取的人数填入表.
(Ⅱ) 在(Ⅰ)中,若A,C两组被抽到的评委中各有2人支持1号歌手,现从这两组被抽到的评委中分别任选1人,求这2人都支持1号歌手的概率.
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 200 | 150 | 50 |
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 200 | 150 | 50 |
| 抽取人数 | 6 |
14.从六个数1,3,4,6,7,9中任取4个数,则这四个数的平均数是5的概率为( )
| A. | $\frac{1}{20}$ | B. | $\frac{1}{15}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
12.设复数z1=-1+3i,z2=1+i,则$\frac{{{z}_{1}+z}_{2}}{{z}_{1}-{z}_{2}}$=( )
| A. | -1-i | B. | 1+i | C. | 1-i | D. | -1+i |
