题目内容
5.已知关于x的方程$\sqrt{1-{x}^{2}}$=x+m没有实数根,则m的取值范围是m>$\sqrt{2}$,或m<-1.分析 设f(x)=$\sqrt{1-{x}^{2}}$和y=x+m,利用数形结合先求出方程$\sqrt{1-{x}^{2}}$=x+m有实数根的取值范围,即可得到结论.
解答 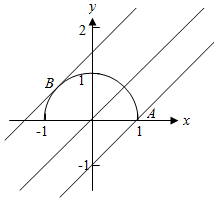 解:设f(x)=$\sqrt{1-{x}^{2}}$和y=x+m,
解:设f(x)=$\sqrt{1-{x}^{2}}$和y=x+m,
则f(x)的轨迹是以原点为圆心,半径为1的圆的上半部分,
作出函数f(x)的图象如图
当直线y=x+m经过点A(1,0)时,1+m=0,得m=-1,
当直线y=x+m在第二象限与圆相切时,m>0,
圆心到直线的距离d=$\frac{|m|}{\sqrt{2}}$=1,得|m|=$\sqrt{2}$,即m=±$\sqrt{2}$,
∵m>0,∴m=$\sqrt{2}$,
则方程$\sqrt{1-{x}^{2}}$=x+m有实数根,
则-1≤m≤$\sqrt{2}$,
则若方程没有实数解,
则m>$\sqrt{2}$,或m<-1,
故答案为:m>$\sqrt{2}$,或m<-1
点评 本题主要考查函数与方程的应用,利用数形结合进行转化,先求出两个函数有交点的取值范围,然后进行转化求解是解决本题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
20.已知集合M={0,1,2},N={x|-1≤x≤1,x∈Z},则( )
| A. | M⊆N | B. | N⊆M | C. | M∩N={0,1} | D. | M∪N=N |
10.i是虚数单位,若复数z满足zi=-1+i,则复数z的实部与虚部的和是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
17.直线x+y+1=0与坐标轴围成的三角形的面积为( )
| A. | 1 | B. | 2 | C. | 3 | D. | $\frac{1}{2}$ |
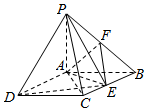 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动.
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动. 如图,在△ABC中,∠ABC=90°,AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°.
如图,在△ABC中,∠ABC=90°,AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°.