Question

设C：y＝x²(x＞0)上的点为P₀(x₀，y₀)，过P₀作曲线C的切线与x轴交于Q₁，过Q₁作平行于y轴的直线与曲线C交于P₁(x₁，y₁)，然后再过P₁作曲线C的切线与x轴交于Q₂，过Q₂作平行于y轴的直线与曲线C交于P₂(x₂，y₂)，依次类推，作出以下各点：Q₃，P₃，…，P_n，Q_n+1，…．已知x₀＝2，设P_n(x_n，y_n)(n∈N)．

(1)设x_n＝f(n)，求f(n)的表达式；

(2)求g(n)＝；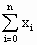

(3)设S_n＝[g(n)－4]log₂f(n)．若n＞2，求证：－1≤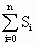＜0．

Answer 1

答案：
解析：

解　　(1)由y＝x2得：＝2x． 　　设C：直线PnQn+1方程y－＝2xn(x－xn)，令y＝0，得xn+1＝xn－xn＝xn， 　　即xn+1＝xn，得xn＝f(n)＝2()n＝()n－1(n＝0，1，2，3，…)． 　　(2)g(n)＝2＋1＋＋…＋()n－1＝4－()n－1． 　　(3)Sn＝[g(n)－4]log2f(n)＝－()n－1log2()n－1＝(n－1)()n－1． 　　令Tn+1＝＝－2＋0＋1×＋…＋(n－1)×()n－1．(1)则 　　(2) 　　(1)－(2)，得Tn+1＝－1＋0＋1×＋1×()2＋…＋1×()n－1－(n－1)×()n． 　　中间n－1项求和，整理得 Tn+1＝＝－，又Tn+1－Tn＝－ 　　所以数列{Tn}是单调递增数列． 　　因为n＞2，所以当n＝3时，取得最小值T3＝－1，所以－1≤＜0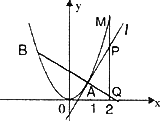．