题目内容
已知函数f(x)＝2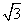
·sin
cos－sin(x＋π)．
(1) 求f(x)的最小正周期；
(2) 若将f(x)的图象向右平移
个单位，得到函数g(x)的图象，求函数g(x)在区间[0，π]上的最大值和最小值．
解：(1) 因为f(x)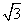＝sin
＋sinx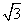＝cosx＋sinx＝2
＝2sin
，所以f(x)的最小正周期为2π.
(2) ∵ 将f(x)的图象向右平移个单位，得到函数g(x)的图象，∴ g(x)＝f
＝2sin
＝2sin
.∵ x∈[0，π]，∴ x＋∈
，
∴ 当x＋＝
，即x＝
时，sin
＝1，g(x)取得最大值2.
当x＋＝
，即x＝π时，sin＝－
，g(x)取得最小值－1.
练习册系列答案
阅读快车系列答案
相关题目
，且
，则cos2θ＝________．
＝
，则sinθ＋cosθ＝________．
个单位后，与函数y＝sin
的图象重合，则φ＝________．
，则sinα＝________．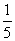
.
＋
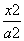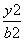＝1(a>b>0)的离心率为
，且过点P
，A为上顶点，F为右焦点．点Q(0，t)是线段OA(除端点外)上的一个动点，