题目内容
2．如图，在正方体ABCDA1B1C1D1中，求证：平面AB1D1∥平面C1BD；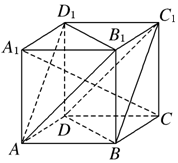
分析 利用直方图与平行四边形的性质可得：BC1∥AD1，利用线面平行的判定定理可得BC1∥平面AB1D1，同理可得：BD∥平面AB1D1，即可证明：平面C1BD∥平面AB1D1．
解答 证明：∵ABCD-A1B1C1D1为正方体，
∴在平行四边形ABC1D1中，BC1∥AD1，
又AD1?平面AB1D1，BC1?平面AB1D1，
∴BC1∥平面AB1D1，
同理可得：BD∥平面AB1D1，且BC1∩BD=B，
∴平面C1BD∥平面AB1D1．
点评 本题考查了空间位置关系与空间角、线面、面面平行的判定与性质定理、线面、面面垂直的判定与性质定理、空间角，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
7．已知函数f（x）满足$f（x）-2f（\frac{1}{x}）=\frac{3}{x^2}$，则f（x）的最大值是（ ）
| A． | -2 | B． | $-2\sqrt{2}$ | C． | 2 | D． | $2\sqrt{2}$ |
11．
过椭圆C：$\frac{{x_{\;}^2}}{{a_{\;}^2}}+\frac{{y_{\;}^2}}{{b_{\;}^2}}=1$（a＞b＞0）的左顶点A且斜率为k的直线交椭圆C于另一点B．且点B在x轴上射影恰好为右焦点F，若$\frac{1}{6}＜|k|＜\frac{1}{3}$，则椭圆C的离心率取值范围是（ ）
过椭圆C：$\frac{{x_{\;}^2}}{{a_{\;}^2}}+\frac{{y_{\;}^2}}{{b_{\;}^2}}=1$（a＞b＞0）的左顶点A且斜率为k的直线交椭圆C于另一点B．且点B在x轴上射影恰好为右焦点F，若$\frac{1}{6}＜|k|＜\frac{1}{3}$，则椭圆C的离心率取值范围是（ ）| A． | （$\frac{2}{3}，\frac{5}{6}$） | B． | （$\frac{2}{3}$，1） | C． | （$\frac{1}{4}，\frac{3}{4}$） | D． | （$\frac{1}{4}，\frac{5}{4}$） |