题目内容
已知向量 向量
向量 与向量
与向量 的夹角为
的夹角为 ,且
,且 。
。
(1 )求向量 ;
;
(2)若向量 与
与 共线,向量
共线,向量 ,其中
,其中 、
、 为
为 的内角,且
的内角,且 、
、 、
、 依次成等差数列,求
依次成等差数列,求 的取值范围.
的取值范围.
(1) 或
或 .(2)
.(2) .
.
解析试题分析:(1)设 .由
.由 ,得
,得 ① 2分
① 2分
又向量 与向量
与向量 的夹角为
的夹角为 ,得
,得 ② 4分
② 4分
由①、②解得 或
或 ,
, 或
或 . 5分
. 5分
(2)向量 与
与 共线知
共线知 ; 6分
; 6分
由 知
知 . 7分
. 7分 , 8分
, 8分 … 9分
… 9分 .………11分
.………11分 , 12分
, 12分
得 ,即
,即 , 13分
, 13分 . 14分
. 14分
考点:本题主要考查平面向量的坐标运算,模的计算,和差倍半公式,三角函数图象和性质。
点评:典型题,本题解答思路明确,首先进行向量的坐标运算,利用两角和与差的三角函数公式进行“化一”,进一步研究函数的图象和性质。模的计算中“化模为方”是常用转化方法。

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
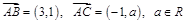
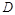 为
为 的中点,
的中点,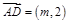 ,求
,求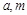 的值;
的值; 是以
是以 为斜边的直角三角形,求
为斜边的直角三角形,求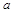 的值.
的值. .
. ,求
,求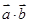 的值;
的值;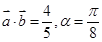 ,且
,且 ,求
,求 的值.
的值.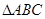 的三个内角
的三个内角 所对的边分别为a,b,c,向量
所对的边分别为a,b,c,向量 ,
, ,且
,且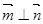 .
. 的大小;
的大小; ,
,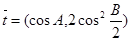 ,试求
,试求 的取值范围
的取值范围 中,
中, 为
为 中点,
中点,  ,
, ,设
,设


 表示
表示 ; (Ⅱ)试用
; (Ⅱ)试用 .
.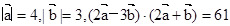 ,
,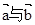 的夹角
的夹角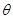 ; (2)求
; (2)求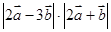 的值.
的值. 是两个不共线的向量,,若A、B、D三点共线,求k的值.
是两个不共线的向量,,若A、B、D三点共线,求k的值. ,满足
,满足  ,
, 与
与 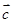 的夹角为
的夹角为 B.90
B.90 =(2,-1),向量
=(2,-1),向量 与
与 ,则
,则