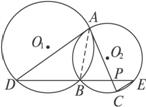
题目内容
已知点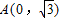 和圆O1:
和圆O1: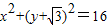 ,点M在圆O1上运动,点P在半径O1M上,且|PM|=|PA|,求动点P的轨迹方程.
,点M在圆O1上运动,点P在半径O1M上,且|PM|=|PA|,求动点P的轨迹方程.
【答案】分析:根据题意,可得|O1P|+|PA|=|O1M|=4,得到P的轨迹是以点A(0,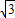 ),O1(0,
),O1(0,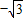 )为焦点的椭圆.根据椭圆的基本概念求出椭圆方程,即可得到动点P的轨迹方程.
)为焦点的椭圆.根据椭圆的基本概念求出椭圆方程,即可得到动点P的轨迹方程.
解答:解:由题意,可得
圆O1: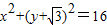 是以O1(0,-
是以O1(0,-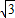 )为圆心,半径r=4的圆
)为圆心,半径r=4的圆
∵点P在半径O1M上,且|PM|=|PA|,
∴|O1P|+|PA|=|O1P|+|PM|=|O1M|=4,
可得点P到A(0,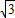 ),O1(0,
),O1(0,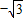 )的距离之和为4(常数)
)的距离之和为4(常数)
因此,点P的轨迹是以点A(0,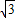 ),O1(0,
),O1(0,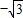 )为焦点的椭圆,
)为焦点的椭圆,
∵焦点在y轴上,c=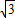 且2a=4,
且2a=4,
∴a=2得a2=4,b2=a2-c2=4-3=1,椭圆方程为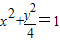
综上所述,点P的轨迹方程为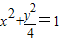 .
.
点评:本题给出圆O1上动点P和定点A,求点P的轨迹方程,着重考查了椭圆的标准方程和动点轨迹方程的求法等知识,属于基础题.
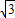 ),O1(0,
),O1(0,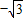 )为焦点的椭圆.根据椭圆的基本概念求出椭圆方程,即可得到动点P的轨迹方程.
)为焦点的椭圆.根据椭圆的基本概念求出椭圆方程,即可得到动点P的轨迹方程.解答:解:由题意,可得
圆O1:
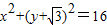 是以O1(0,-
是以O1(0,-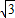 )为圆心,半径r=4的圆
)为圆心,半径r=4的圆∵点P在半径O1M上,且|PM|=|PA|,
∴|O1P|+|PA|=|O1P|+|PM|=|O1M|=4,
可得点P到A(0,
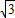 ),O1(0,
),O1(0,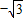 )的距离之和为4(常数)
)的距离之和为4(常数)因此,点P的轨迹是以点A(0,
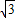 ),O1(0,
),O1(0,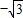 )为焦点的椭圆,
)为焦点的椭圆,∵焦点在y轴上,c=
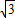 且2a=4,
且2a=4,∴a=2得a2=4,b2=a2-c2=4-3=1,椭圆方程为
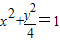
综上所述,点P的轨迹方程为
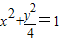 .
.点评:本题给出圆O1上动点P和定点A,求点P的轨迹方程,着重考查了椭圆的标准方程和动点轨迹方程的求法等知识,属于基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 和圆O1:
和圆O1: ,点M在圆O1上运动,点P在半径O1M上,且|PM|=|PA|,求动点P的轨迹方程.
,点M在圆O1上运动,点P在半径O1M上,且|PM|=|PA|,求动点P的轨迹方程.