Question

如图2-5-11，已知⊙O₁和⊙O₂相交于点A、B，过点A作⊙O₁的切线交⊙O₂于点C，过点B作两圆的割线，分别交⊙O₁、⊙O₂于点D、E，DE与AC相交于点P.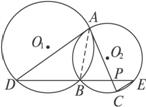

图2-5-11

（1）求证：AD∥EC；

（2）若AD是⊙O₂的切线，且PA=6，PC=2，BD=9，求AD的长.

Answer 1

思路分析：（1）连结AB，利用⊙O₁的弦切角∠BAC过渡来证明∠D=∠E.（2）设BP=x，PE=y，利用相交弦定理和AD∥EC可以列出关于x、y的方程组，求出x、y，再用切割线定理求AD.

（1）证明：连结AB.

∵AC为⊙O₁的切线，∴∠BAC=∠D.

又∵∠BAC=∠E,∴∠D=∠E.

∴AD∥EC.

（2）解：设PB=x，PE=y,∵AP=6，PC=2，∴xy=12.①

∵AD∥EC，∴，即.

∴9+x=3y.②

由①②解得

（舍去）.

∴DE=9+x+y=16.

∵AD为⊙O₂的切线，

∴AD²=DB·DE=9×16.

∴AD=12.

    深化升华 本例综合运用了弦切角定理、相交弦定理、切割线定理和平行线分线段成比例定理，综合性较强.在这里应强调的是利用代数方法解决几何问题，特别是利用方程进行计算、求值等，要建立运用数形结合的思想.